
如图,已知AB为⊙O的直径,CD是弦,且AB CD于点E.连接AC、OC、BC.
CD于点E.连接AC、OC、BC.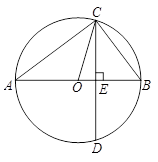
(1)求证:∠ACO=∠BCD.
(2)若BE=3,CD=8,求⊙O的直径.
证明:(1)∵AB为⊙O的直径,CD是弦,且AB CD于E,
CD于E,
∴CE=ED, 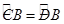
∴ BCD=
BCD= BAC.
BAC.
∵OA=OC,
∴ OAC=
OAC= OCA .
OCA .
∴ ACO=
ACO= BCD.
BCD.
(2) ∵CD=8,
∴CE=ED=4,
在Rt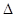 BCE中,
BCE中,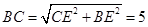 .
.
∵AB为⊙O的直径,
∴∠ACB=∠BEC=90°.
∵∠B=∠B,
∴△CBE∽△ABC.
∴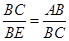 .
.
∴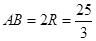
答:⊙O的直径为 .
.
解析试题分析:(1)根据垂径定理得出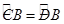 ,根据圆周角定理得出∠BCD=∠CAB,根据等腰三角形的性质得出∠CAB=∠ACO,即可得出答案;(2)根据垂径定理求出CE,根据勾股定理求出BC,证出△BCE和△BCA相似,即可得出比例式,代入计算即可求出答案.
,根据圆周角定理得出∠BCD=∠CAB,根据等腰三角形的性质得出∠CAB=∠ACO,即可得出答案;(2)根据垂径定理求出CE,根据勾股定理求出BC,证出△BCE和△BCA相似,即可得出比例式,代入计算即可求出答案.
考点:垂径定理;勾股定理;等腰三角形性质;相似三角形的性质和判定.
点评:本题主要考查了相似三角形的性质和判定,圆周角定理,垂径定理,等腰三角形性质,勾股定理等知识点的应用,解答本题的关键是培养学生综合运用定理进行推理和计算的能力.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源:2014-2015学年江苏省九年级上学期期中调研考试数学试卷(解析版) 题型:填空题
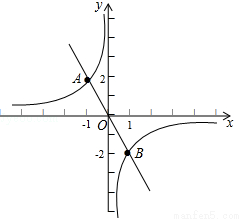
如图,正比例函数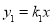 和反比例函数
和反比例函数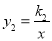 的图象交于A(﹣1,2)、B(1,﹣2)两点,若
的图象交于A(﹣1,2)、B(1,﹣2)两点,若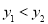 ,则x的取值范围是 .
,则x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级上学期期中考试数学试卷(解析版) 题型:选择题
已知圆锥的底面半径为4cm,母线长为5cm,则这个圆锥的侧面积是( )
A.20πcm2 B.20cm2 C.40πcm2 D.40cm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com