
【题目】如图,已知点A(0,1),C(4,3),E![]() ,P是以AC为对角线的矩形ABCD内部(不在各边上)的一动点,点D在y轴上,抛物线y=ax2+bx+1以P为顶点.
,P是以AC为对角线的矩形ABCD内部(不在各边上)的一动点,点D在y轴上,抛物线y=ax2+bx+1以P为顶点.
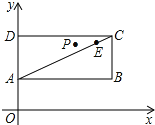
(1)求证:A、C、E三点共线;
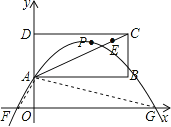
(2)设抛物线y=ax2+bx+1与x轴有交点F、G(F在G的左侧),△GAO与△FAO的面积差为3,且这条抛物线与线段AE有两个不同的交点,试确定a、b的取值范围.
【答案】(1)证明见解析;(2)﹣![]() <a<﹣
<a<﹣![]() ,
,![]() <b<
<b<![]() .
.
【解析】
试题分析:(1)说明点A、C、E在一条直线上,只要求出过A、C的直线的解析式,然后判断E是否满足函数的解析式就可以;
(2)连接GA、FA,已知△GAO与△FAO的面积差为3,而这两个三角形的高相同是OA的长,等于1,因而就可以得到OG与OF的长度的一个关系式.抛物线y=ax2﹣6ax+1的顶点可以用a表示出来,顶点P在矩形ABCD的内部,即可以求出a的取值范围.
解:(1)由题意,A(0,1)、C(4,3)两点确定的直线解析式为:y=![]() x+1,
x+1,
将点E的坐标(![]() ,
,![]() ),代入y=
),代入y=![]() x+1中,左边=
x+1中,左边=![]() ,右边=
,右边=![]() ×
×![]() +1=
+1=![]() ,
,
∵左边=右边,
∴点E在直线y=![]() x+1上,
x+1上,
即点A、C、E在一条直线上;
(2)连接GA、FA.
∵S△GAO﹣S△FAO=3
∴![]() GOA0=
GOA0=![]() FOAO=3.
FOAO=3.
∵OA=1,
∴GO﹣FO=6.
设F(x1,0),G(x2,0),
则x1、x2是方程ax2+bx+1=0的两个根,且x1<x2,
又∵a<0
∴x1x2=![]() <0,
<0,
∴GO=x2、FO=﹣x1
∴x2﹣(﹣x1)=6,即x2+x1=6
∵x2+x1=﹣![]() ,
,
∴﹣![]() =6,
=6,
∴抛物线的解析式为:y=ax2﹣6ax+1,其顶点P的坐标为(3,1﹣9a)
∵顶点P在矩形ABCD的内部,
∴1<1﹣9a<3,
∴﹣![]() <a<0①
<a<0①
由方程组 ,
,
得:ax2﹣(6a+![]() )x=0,
)x=0,
∴x=0或x=![]() =6+
=6+![]() ,
,
当x=0时,即抛物线与线段AE交于点A,而这条抛物线与线段AE有两个不同的交点,
则有:0<6+![]() <
<![]() ,
,
解得:﹣![]() ≤a<﹣
≤a<﹣![]() ,
,
综合①②,得﹣![]() <a<﹣
<a<﹣![]() ,
,
∵b=﹣6a,
∴![]() <b<
<b<![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1所示,边长为a的大正方形中有一个边长为b的小正方形,如图2是由图1中阴影部分拼成的一个长方形。
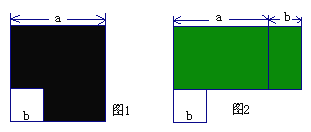
(1)请你分别表示出这两个图形中阴影部分的面积: , ;
(2)请问以上结果可以验证哪个乘法公式? ;
(3)试利用这个公式计算:
①、![]() ②、
②、 ![]()
③、![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一张对边互相平行的纸条,折成如图所示,EF是折痕,若∠EFB=32°,则下列结论正确的有( )
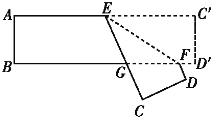
(1)∠C′EF=32°;(2)∠AEC=148°;
(3)∠BGE=64°; (4)∠BFD=116°.
(A)1个 (B)2个 (C)3个 (D)4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算正确的是( )
A.2a3+3a3=5a6
B.(x4)2=x6
C.﹣2m(m﹣3)=﹣2m2﹣6m
D.(3a+2)(3a﹣2)=9a2﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B,C,D,E五名学生猜测自己的数学成绩. A说:“如果我得优,那么B也得优.” B说:“如果我得优,那么C也得优.” C说:“如果我得优,那么D也得优.” D说:“如果我得优,那么E也得优.” 大家都没有说错,但只有三个人得优,请问:得优的是哪三个人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点的门票价格规定如下表
购票人数 | 1﹣50人 | 51﹣100人 | 100人以上 |
每人门票价 | 12元 | 10元 | 8元 |
某校八年(一)、(二)两班共100多人去游览该景点,其中(一)班不足50人,(二)班多于50人,如果两班都以班为单位分别购票,则一共付款1126元.如果以团体购票,则需要付费824元,问:
(1)两班各有多少名学生?
(2)如果你是学校负责人,你将如何购票?你的购票方法可节省多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com