
分析 (1)原式利用立方公式和因式分解变形为x3-1-(x+1)(x2-x+1),再利用立方公式变形为x3-1-(x3+1),再去括号合并得到结果为常数,即可得到结果与x值无关.
(2)先变为指数相同,再比较底数的大小即可求解.
解答 解:(1)(x-1)(x2+x+1)-(x2+1)(x+1)+x(x+1)
=x3-1-(x+1)(x2-x+1)
=x3-1-(x3+1)
=x3-1-x3-1
=-2,
∵结果为常数,
∴无论x为何值,代数式(x-1)(x2+x+1)-(x2+1)(x+1)+x(x+1)的值等于一个常数.
(2)∵3555=243111,4444=256111,5333=125111,
256>243>125,
∴4444>3555>5333.
点评 此题考查了整式的加减,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
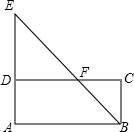 如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )
如图,点F是矩形ABCD的边CD上一点,射线BF交AD的延长线于点E,则下列结论错误的是( )| A. | $\frac{ED}{BC}$=$\frac{EF}{FB}$ | B. | $\frac{DE}{AD}$=$\frac{DF}{AB}$ | C. | $\frac{BC}{DE}$=$\frac{CF}{DF}$ | D. | $\frac{BF}{BE}$=$\frac{BC}{AE}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com