
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 把2,12,27,n分解为两个正整数的积的形式,找到相差最少的两个数,让较小的数除以较大的数,看结果是否与所给结果相同.
解答 解:(1)2可以分解成1×2,所以F(2)=$\frac{1}{2}$;故(1)正确.
(2)12可以分解成1×12,2×6,3×4这三种,这几种分解中4和3的差的绝对值最小,所以F(12)=$\frac{3}{4}$,故(2)正确.
(3)27可以分解成1×27,3×9这两种,其中3和9的绝对值较小,又3<9,所以F(27)=$\frac{3}{9}$=$\frac{1}{3}$,故(3)错误.
(4)n是一个整数的平方,则F(n)=$\frac{n}{n}$=1,故(4)正确.
所以正确的说法是(1)、(2)、(4).
故选:C.
点评 本题考查了因式分解的应用,解决本题的关键是理解此题的定义:所有这种分解中两因数之差的绝对值最小,F(n)=$\frac{p}{q}$(p≤q).


科目:初中数学 来源: 题型:解答题
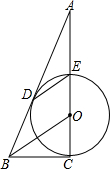 如图,CE是⊙O的直径,BD切⊙O于点D,DE∥BO,CE的延长线交BD于点A.
如图,CE是⊙O的直径,BD切⊙O于点D,DE∥BO,CE的延长线交BD于点A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
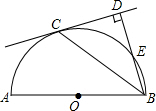 如图,AB是半圆O的直径,C是半圆O上的一点,BD与过点C的直线相互垂直,垂足为点D,BD与半圆O交于点E,且BC平分∠DBA.
如图,AB是半圆O的直径,C是半圆O上的一点,BD与过点C的直线相互垂直,垂足为点D,BD与半圆O交于点E,且BC平分∠DBA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a(1+x)2 | B. | a(1+x%)2 | C. | a+a•x% | D. | a+a•(x%)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
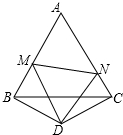 如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120度.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN.
如图,△ABC是边长为3的等边三角形,△BDC是等腰三角形,且∠BDC=120度.以D为顶点作一个60°角,使其两边分别交AB于点M,交AC于点N,连接MN.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com