练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    不等式组的解集是：

    A、                  B、         C、     D、无解


    C


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，数轴上A、B两点分别对应实数a、b，则下列结论正确的是

        A．       B．

        C．                         D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知关于x的一元二次方程：．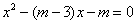

    （1）试判断原方程根的情况；（4分）

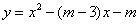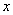    （2）若抛物线与轴交于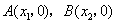两点，则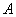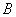，两点间的距离是否存在最大或最小值？若存在，求出这个值；若不存在，请说明理由．

    （友情提示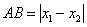：）（6分）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图是“赵爽弦图”，△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形，四边形ABCD和EFGH都是正方形，如果AB＝10，EF＝2，那么AH等于　　　　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在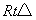ABC中，∠C＝90º，BD是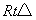ABC的一条角一平分线，点O、E、F分别在BD、BC、AC上，且四边形OECF是正方形，

    （1）求证：点O在∠BAC的平分线上；

    （2）若AC＝5，BC＝12，求OE的长

    　　　　　　　　　　　　　　　　　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若两个扇形满足弧长的比等于它们半径的比，则这称这两个扇形相似。如图，如果扇形AOB与扇形是相似扇形，且半径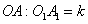(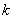为不等于0的常数)。那么下面四个结论：

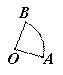
    ①∠AOB＝∠；②△AOB∽△；③；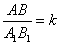

    ④扇形AOB与扇形的面积之比为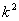。成立的个数为：

    A、1个　　　　B、2个　　　　　C、3个　　　　D、4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABC中，∠B＝40°，三角形的外角∠DAC和∠ACF的平分线交于点E，则∠AEC＝　　　　　　度。

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一个角的度数为20°，则它的补角的度数为        ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知抛物线y＝x2＋c与x轴交于A(－1，0)，B两点，交y轴于点C

    (1) 求抛物线的解析式

    (2) 点E(m，n)是第二象限内一点，过点E作EF⊥x轴交抛物线于点F，过点F作FG⊥y轴于点G，连接CE、CF，若∠CEF＝∠CFG，求n的值并直接写出m的取值范围（利用图1完成你的探究）

    (3) 如图2，点P是线段OB上一动点（不包括点O、B），PM⊥x轴交抛物线于点M，∠OBQ＝∠OMP，BQ交直线PM于点Q，设点P的横坐标为t，求△PBQ的周长

           

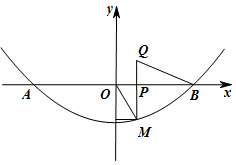
    查看答案和解析>>

    同步练习册答案