
【题目】平行四边形ABCD中,对角线AC,BD相交于点O,若E、F是AC上两动点,E、F分别
从A、C两点同时以1cm/s的相同的速度向C、A运动.

(1)四边形DEBF是平行四边形吗?说明你的理由.
(2)若BD=10cm,AC=16cm,当运动时间t为多少时,
四边形DEBF为矩形.
【答案】(1)四边形DEBF是平行四边形(2) 当运动时间t为3或13s时.四边形DEBF为矩形
【解析】试题分析:(1)由平行四边形ABCD中,可得OA=OC,OB=OD,又由若E、F是AC上两动点,E、F分别从A、C两点同时以1cm/s的相同的速度向C、A运动,易得AE=CF,即可得OE=OF,则可判定四边形DEBF是平行四边形;
(2)由四边形DEBF是平行四边形,可得当EF=BD时,四边形DEBF为矩形,即可得方程:16-t-t=10或2t-16=10,继而求得答案.
解:(1)四边形DEBF是平行四边形.
理由:∵四边形ABCD是平行四边形.
∴OA=OC.OB=OD.
∵E.F是AC上两动点.E.F分别从A.C两点同时以1cm/s的相同的速度向C.A运动.
∴AE=CF.
∴OE=OF.
∴四边形DEBF是平行四边形;
(2)根据题意得:AE=CF=tcm.
∵四边形DEBF是平行四边形.
∴当EF=BD时.四边形DEBF为矩形.
即AC-AE-CF=BD.
∴16-t-t=10或2t-16=10
解得:t=3.或t=13
∴当运动时间t为3或13s时.四边形DEBF为矩形


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,﹣1),P5(2,﹣1),P6(2,0),…,则点P2017的坐标是( )
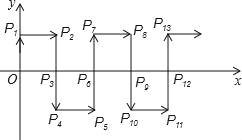
A. (671,﹣1) B. (672,0) C. (672,1) D. (672,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=1,FD=2,则BC的长为( ) 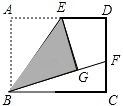
A.3 ![]()
B.2 ![]()
C.2 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠ABC=30°,AC=1,将△ABC绕点C逆时针旋转至△A′B′C,使得点A′恰好落在AB上,连接BB′,则BB′的长度为
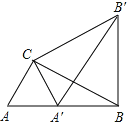
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解初二年级480名学生到校上学的方式,在初二随机抽取了若干名学生进行问卷调查.问卷给出了五种上学方式供学生选择,每人只能选一项,且不能不选.将调查得到的结果绘制成如图所示的条形统计图和扇形统计图(均不完整).


⑴问:在这次调查中,一共抽取了多少名学生?
⑵补全条形统计图;
⑶估计该校初二年级学生中有多少人乘坐公交车上学.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的集合里:
2018,1,-1,-2014,0.5,![]() ,-
,-![]() ,-0.75,0,20%,
,-0.75,0,20%,![]()
整数集合:{____________________…};正分数集合:{________________…};
负分数集合:{________________…};正数集合:{__________________…};
负数集合:{__________________…}.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某市2016年“书香校园,经典诵读”比赛活动中,有32万名学生参加比赛活动,其中有8万名学生分别获得一、二、三等奖,从获奖学生中随机抽取部分,绘制成不完整的统计表(如表),请根据图表解答下列问题.
获奖等级 | 频数 |
一等奖 | a |
二等奖 | b |
三等奖 | 275 |

(1)表格中a的值为 , b的值为 .
(2)扇形统计图中表示获得一等奖的扇形的圆心角为度.
(3)估计全市有多少名学生获得三等奖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示:
(1)请你根据左图填写右表:
销售公司 | 平均数 | 方差 | 中位数 | 众数 |
甲 | 9 | |||
乙 | 9 | 17.0 | 8 |
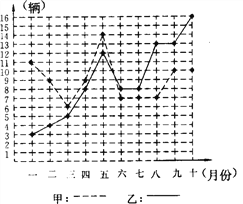
(2)请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:
①从平均数和方差结合看;
②从折线图上甲、乙两个汽车销售公司销售数量的趋势
看(分析哪个汽车销售公司较有潜力).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=6,AD=10,点E是边BC的中点,连接AE,若将△ABE沿AE翻折,点B落在点F处,连接FC,则tan∠BCF= . 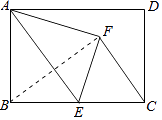
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com