
ЁОЬтФПЁПШчЭМЃЌдкЭЌвЛЦНУцжБНЧзјБъЯЕжаЃЌЖўДЮКЏЪ§yЃНax2ЃЋbxЃЋcгыЖўДЮКЏЪ§yЃН(aЃЋ3)x2ЃЋ(bЃ15)xЃЋcЃЋ18ЕФЭМЯѓгыxжсЕФНЛЕуЗжБ№ЪЧAЃЌBЃЌCЃЎ
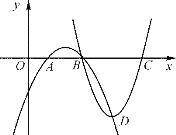
(1)ХаЖЯЭМжаОЙ§ЕуBЃЌDЃЌCЕФЭМЯѓЪЧФФвЛИіЖўДЮКЏЪ§ЕФЭМЯѓЃПЪдЫЕУїРэгЩЃЎ
(2)ЩшСНИіКЏЪ§ЕФЭМЯѓЖМОЙ§ЕуBЁЂDЃЌЧѓЕуBЃЌDЕФКсзјБъЃЎ
(3)ШєЕуDЪЧЙ§ЕуBЁЂDЁЂCЕФКЏЪ§ЭМЯѓЕФЖЅЕуЃЌзнзјБъЮЊЃ2ЃЌЧѓетСНИіКЏЪ§ЕФНтЮіЪНЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃН(aЃЋ3) x2ЃЋ(bЃ15)xЃЋcЃЋ18ЃЛЃЈ2ЃЉ2ЃЌ3ЃЛЃЈ3ЃЉyЃНЃx2 ЃЋ3xЃ2
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтЃЌСНИіХзЮяЯпЃЌвЛИіПЊПкЯђЯТЃЌвЛИіПЊПкЯђЩЯЃЌдђБШНЯЖўДЮЯюЯЕЪ§МДПЩЕУЕНД№АИЃЛ
ЃЈ2ЃЉНсКЯСНИіКЏЪ§НтЮіЪНЃЌзщГЩЗНГЬзщЃЌЧѓГіxЕФжЕЃЌМДПЩЕУЕНЕуBЁЂDЕФКсзјБъЃЛ
ЃЈ3ЃЉИљОнЬтвтЃЌЕУЕНЖЅЕуDЕФзјБъЃЌШЛКѓАбЕуBЃЈ2ЃЌ0ЃЉДњШыЃЌМДПЩЕУЕННтЮіЪН.
НтЃКЃЈ1ЃЉИљОнЬтвтЃЌгЩХзЮяЯпПЊПкЃЌвЛИіПЊПкЯђЯТЃЌвЛИіПЊПкЯђЩЯЃЌ
ЁпaЃЋ3>aЃЌ
ЁрОЙ§BЁЂDЁЂCЕФЭМЯѓЪЧЃКyЃН(aЃЋ3) x2ЃЋ(bЃ15)xЃЋcЃЋ18ЕФЭМЯѓЃЎ
ЃЈ2ЃЉНтЗНГЬзщ
ећРэЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃКx1ЃН2ЃЌx2ЃН3ЃЌ
ЁрЕуBЃЌDЕФКсзјБъЗжБ№ЮЊ2ЃЌ3ЃЛ
ЃЈ3ЃЉгЩЬтПЩжЊЃЌЕуDзјБъЮЊЃЈ3ЃЌЃ2ЃЉЃЌ
ЩшЫљЧѓНтЮіЪНЮЊЃКyЃН a (xЃ3)2Ѓ2ЃЌ
АбЕуBЕФзјБъ(2ЃЌ0)ДњШыЃЌдђ
![]() ЃЌ
ЃЌ
НтЕУЃКaЃН2ЃЌ
Ёр![]() ЃЌ
ЃЌ
МДyЃН2x2Ѓ12xЃЋ16ЃЛ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрзѓБпХзЮяЯпЕФНтЮіЪНЮЊЃКyЃНЃx2 ЃЋ3xЃ2ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИХФюШЯЪЖ
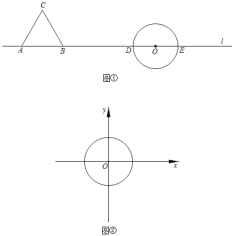
ЦНУцФкЃЌMЮЊЭМаЮTЩЯШЮвтвЛЕуЃЌNЮЊЁбOЩЯШЮвтвЛЕуЃЌНЋMЁЂNСНЕуМфОрРыЕФзюаЁжЕГЦЮЊЭМаЮTЕНЁбOЕФЁАзюНќОрРыЁБЃЌМЧзїdЃЈTЉЁбOЃЉЃЎР§ШчЭМЂйЃЌдкжБЯпlЩЯгаAЁЂBЁЂOШ§ЕуЃЌвдABЮЊвЛБпзїЕШБпЁїABCЃЌвдЕуOЮЊдВаФзїдВЃЌгыlНЛгкDЁЂEСНЕуЃЌШєНЋЁїABCМЧЮЊЭМаЮTЃЌдђBЁЂDСНЕуМфЕФОрРыГЦЮЊЭМаЮTЕНЁбOЕФЁАзюНќОрРыЁБЃЎ
Ъ§бЇРэНт
ЃЈ1ЃЉдкжБЯпlЩЯгаAЁЂBСНЕуЃЌвдЕуAЮЊдВаФЃЌ3ЮЊАыОЖзїЁбAЃЌНЋЕуBМЧЮЊЭМаЮTЃЌШєdЃЈTЉЁбAЃЉЃН1ЃЌдђABЃНЁЁ ЁЁЃЎ
ЃЈ2ЃЉШчЭМЂкЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвдOЃЈ0ЃЌ0ЃЉЮЊдВаФЃЌАыОЖЮЊ2зїдВЃЎ
ЂйНЋЕуCЃЈ4ЃЌ3ЃЉМЧЮЊЭМаЮTЃЌдђdЃЈTЉЁбOЃЉЃНЁЁ ЁЁЃЎ
ЂкНЋвЛДЮКЏЪ§yЃНkx+2![]() ЕФЭММЧЮЊЭМаЮTЃЌШєdЃЈTЉЁбOЃЉЃО0ЃЌЧѓkЕФШЁжЕЗЖЮЇЃЎ
ЕФЭММЧЮЊЭМаЮTЃЌШєdЃЈTЉЁбOЃЉЃО0ЃЌЧѓkЕФШЁжЕЗЖЮЇЃЎ
ЭЦЙудЫгУ
ЃЈ3ЃЉдкЦНУцжБНЧзјБъЯЕжаЃЌPЕФзјБъЮЊЃЈtЃЌ0ЃЉЃЌЁбPЕФАыОЖЮЊ2ЃЌDЁЂEСНЕуЕФзјБъЗжБ№ЮЊЃЈЉ8ЃЌ8ЃЉЁЂЃЈЉ8ЃЌЉ8ЃЉЃЌНЋЁЯDOEМЧЮЊЭМаЮTЃЌШєdЃЈTЉЁбPЃЉЃН1ЃЌдђtЃНЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
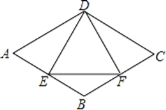
ЁОЬтФПЁПШчЭМЃЌдкСтаЮABCDжаЃЌEЪЧABБпЩЯвЛЕуЃЌЧвЁЯA=ЁЯEDF=60ЁуЃЌгаЯТСаНсТлЃКЂйAE=BFЃЛЂкЁїDEFЪЧЕШБпШ§НЧаЮЃЛЂлЁїBEFЪЧЕШбќШ§НЧаЮЃЛЂмЁЯADE=ЁЯBEFЃЌЦфжаНсТле§ШЗЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
A.3
B.4
C.1
D.2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃОХФъМЖбЇЩњаЁРіЃЌаЁЧПКЭаЁКьЕНФГГЌЪаВЮМгСЫЩчЛсЪЕМљЛюЖЏЃЌдкЛюЖЏжаЫћУЧВЮгыСЫФГжжЫЎЙћЕФЯњЪлЙЄзїЃЌвбжЊИУЫЎЙћЕФНјМлЮЊ8дЊ/ЧЇПЫЃЌЯТУцЪЧЫћУЧдкЛюЖЏНсЪјКѓЕФЖдЛА.
аЁРіЃКШчЙћвд10дЊ/ЧЇПЫЕФМлИёЯњЪлЃЌФЧУДУПЬьПЩЪлГі300ЧЇПЫ.
аЁЧПЃКШчЙћвд13дЊ/ЧЇПЫЕФМлИёЯњЪлЃЌФЧУДУПЬьПЩЛёШЁРћШѓ750дЊ.
аЁКьЃКЮвЭЈЙ§ЕїВщбщжЄЗЂЯжУПЬьЕФЯњЪлСП![]() (ЧЇПЫ)гыЯњЪлЕЅМл
(ЧЇПЫ)гыЯњЪлЕЅМл![]() (дЊ)жЎМфДцдквЛДЮКЏЪ§ЙиЯЕ.
(дЊ)жЎМфДцдквЛДЮКЏЪ§ЙиЯЕ.
(1)Чѓ![]() (ЧЇПЫ)гы
(ЧЇПЫ)гы![]() (дЊ)
(дЊ)![]() ЕФКЏЪ§ЙиЯЕЪН.
ЕФКЏЪ§ЙиЯЕЪН.
(2)ЕБЯњЪлЕЅМлЮЊКЮжЕЪБЃЌИУГЌЪаЯњЪлетжжЫЎЙћУПЬьЛёЕУЕФРћШѓДя600дЊЃП[РћШѓ=ЯњЪлСПЁС(ЯњЪлЕЅМлЉНјМл)].
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯп![]()
![]() ЕФЖЅЕуЮЊЃЈm
ЕФЖЅЕуЮЊЃЈm![]() ЃЌn
ЃЌn![]() ЃЉХзЮяЯп
ЃЉХзЮяЯп![]() ЕФЖЅЕуЮЊЃЈm
ЕФЖЅЕуЮЊЃЈm![]() ,n
,n![]() ЃЉЃЌШчЙћ
ЃЉЃЌШчЙћ![]() ЃЌФЧУДЮвУЧГЦХзЮяЯп
ЃЌФЧУДЮвУЧГЦХзЮяЯп![]() гы
гы![]() ЙигкЕу
ЙигкЕу![]() жааФЖдГЦЃЌИјГіХзЮяЯпЂй
жааФЖдГЦЃЌИјГіХзЮяЯпЂй![]() ЃЛЂк
ЃЛЂк![]()
(1)ХаЖЯХзЮяЯпЂйгыХзЮяЯпЂкЪЧЗёжааФЖдГЦ?ШєЪЧЃЌЧѓГіЖдГЦжааФЕФзјБъЃЛШєВЛЪЧЃЌЫЕУїРэгЩЃЛ
(2)жБЯпy=mНЛХзЮяЯпЂйгкA. BСНЕуЃЌНЛХзЮяЯпЂкгкC. DСНЕуЃЌШчЙћAB=2CDЃЌЧѓmЕФжЕЃЛ
(3)ЩшХзЮяЯпЂйгыХзЮяЯпЂкЕФЖЅЕуЗжБ№ЮЊMЁЂNЃЌЕуPдкxжсЩЯвЦЖЏЃЌШєЁїMNPЮЊжБНЧШ§НЧаЮЃЌЧѓЕуPзјБъЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЃЈn+1ЃЉИіБпГЄЮЊ2ЕФЕШБпШ§НЧаЮгавЛЬѕБпдкЭЌвЛжБЯпЩЯЃЌЩшЁїB2D1C1ЕФУцЛ§ЮЊS1ЃЌЁїB3D2C2ЕФУцЛ§ЮЊS2ЃЌЁЃЌЁїBЃЈn+1ЃЉDnCnЕФУцЛ§ЮЊSnЃЌдђSn=____ЃЈгУКЌnЕФЪНзгБэЪОЃЉЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕЅЮЛЮЊСЫДДНЈГЧЪаЮФУїЕЅЮЛЃЌзМБИдкЕЅЮЛЕФЧНЃЈЯпЖЮMNЫљЪОЃЉЭтПЊБйвЛДІГЄЗНаЮЕФЩЯЕиНјааТЬЛЏУРЛЏЃЌГ§ЧНЬхЭтШ§УцвЊгУеЄРИЮЇЦ№РДЃЌМЦЛЎгУеЄРИ50УзЃЌЩшABЕФГЄЮЊxУзЃЌГЄЗНаЮЕФУцЛ§ЮЊyЦНЗНУзЃЎ
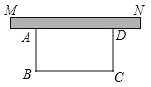
ЃЈ1ЃЉЧыЧѓГіyгыxЕФКЏЪ§ЙиЯЕЪНЃЈВЛашаДГіздБфСПЕФШЁжЕЗЖЮЇЃЉ
ЃЈ2ЃЉВЛПМТЧЧНЬхГЄЖШЃЌЮЪABЕФГЄЮЊЖрЩйЪБЃЌГЄЗНаЮЕФУцЛ§зюДѓЃП
ЃЈ3ЃЉШєЧНЬхГЄЖШЮЊ20УзЃЌЮЪГЄЗНаЮУцЛ§зюДѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈИажЊЃЉаЁССгіЕНСЫетбљвЛЕРЬтЃКвбжЊШчЭМдк![]() жаЃЌ
жаЃЌ![]() дк
дк![]() ЩЯЃЌ
ЩЯЃЌ![]() дк
дк![]() ЕФбгГЄЩЯЃЌ
ЕФбгГЄЩЯЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌЧв
ЃЌЧв![]() ЃЌЧѓжЄ:
ЃЌЧѓжЄ:![]() .
.
аЁССзаЯИЗжЮіСЫЬтжаЕФвбжЊЬѕМўКѓЃЌШчЭМЂкЙ§![]() Еузї
Еузї![]() НЛ
НЛ![]() гк
гк![]() ЃЌНјЖјНтОіСЫИУЮЪЬт.ЃЈВЛашвЊжЄУїЃЉ
ЃЌНјЖјНтОіСЫИУЮЪЬт.ЃЈВЛашвЊжЄУїЃЉ
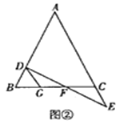
ЃЈЬНОПЃЉШчЭМЂлЃЌдкЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() БпЕФжаЕуЃЌ
БпЕФжаЕуЃЌ![]() гы
гы![]() ЕФбгГЄЯпНЛгкЕу
ЕФбгГЄЯпНЛгкЕу![]() ЃЌЪдЬНОПЯпЖЮ
ЃЌЪдЬНОПЯпЖЮ![]() гы
гы![]() жЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТл.
жЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТл.
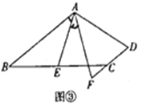
ЃЈгІгУЃЉШчЭМЂлЃЌдке§ЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЮЊ
ЮЊ![]() БпЕФжаЕуЃЌ
БпЕФжаЕуЃЌ![]() ЁЂ
ЁЂ![]() ЗжБ№ЮЊ
ЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() БпЩЯЕФЕуЃЌШє
БпЩЯЕФЕуЃЌШє![]() ЃН1ЃЌ
ЃН1ЃЌ![]() ЃН
ЃН![]() ЃЌЁЯ
ЃЌЁЯ![]() ЃН90ЁуЃЌдђ
ЃН90ЁуЃЌдђ![]() ЕФГЄЮЊ .
ЕФГЄЮЊ .

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкОиаЮABCDжаЃЌEЪЧBCБпвЛЕуЃЌDEЦНЗжЁЯADCЃЌEFЁЮDCНЧADБпгкЕуFЃЌСЌНсBDЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮEFCDЪЧе§ЗНаЮЃЛ
ЃЈ2ЃЉШєBE=1ЃЌED=2![]() ЃЌЧѓBDЕФГЄЃЎ
ЃЌЧѓBDЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com