
����Ŀ��������ʶ
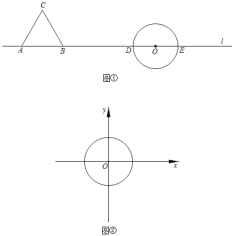
ƽ���ڣ�MΪͼ��T������һ�㣬NΪ��O������һ�㣬��M��N�����������Сֵ��Ϊͼ��T����O�ġ�������롱������d��T����O��������ͼ������ֱ��l����A��B��O���㣬��ABΪһ�����ȱߡ�ABC���Ե�OΪԲ����Բ����l����D��E���㣬������ABC��Ϊͼ��T����B��D�����ľ����Ϊͼ��T����O�ġ�������롱��
��ѧ����
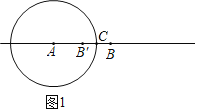
��1����ֱ��l����A��B���㣬�Ե�AΪԲ�ģ�3Ϊ�뾶����A������B��Ϊͼ��T����d��T����A����1����AB���� ����
��2����ͼ������ƽ��ֱ������ϵ�У���O��0��0��ΪԲ�ģ��뾶Ϊ2��Բ��
������C��4��3����Ϊͼ��T����d��T����O������ ����
����һ�κ���y��kx+2![]() ��ͼ��Ϊͼ��T����d��T����O����0����k��ȡֵ��Χ��
��ͼ��Ϊͼ��T����d��T����O����0����k��ȡֵ��Χ��
�ƹ�����
��3����ƽ��ֱ������ϵ�У�P������Ϊ��t��0������P�İ뾶Ϊ2��D��E���������ֱ�Ϊ����8��8��������8����8��������DOE��Ϊͼ��T����d��T����P����1����t���� ����
���𰸡���1��2��4����2����3���ک�1��k��1��k��0����3����3![]() ��3��
��3��
��������
��1������d��T����A����1�ɵ�CB��CB����1����AC��3���ɵó��𰸣�
��2��������OC�����OC�ij��ȼ��ɵó��𰸣�
����ֱ��y��kx+![]() ��y��Ľ���ΪD�����O������E��K������OK��OE�����DK��DE�ij���֤���ı���DEOK�������Σ��õ���ODE����ODK��45����Ȼ�����d��T����O����0���ɵó��𰸣�
��y��Ľ���ΪD�����O������E��K������OK��OE�����DK��DE�ij���֤���ı���DEOK�������Σ��õ���ODE����ODK��45����Ȼ�����d��T����O����0���ɵó��𰸣�
��3�����������Σ�����ͼ31�У�����P�ڡ�DOE�ڲ�ʱ����PM��OD��M������P��K������ͼ32�У�����P�ڡ�DOE�����ʱ���ֱ���⼴�ɣ�
�⣺��1����ͼ1�У�
��d��T����A����1��
��CB��CB����1��
��AC��3��
��AB����2��AB��4��
�ʴ�Ϊ2��4��
��2������ͼ2�У�����OC����O��E��
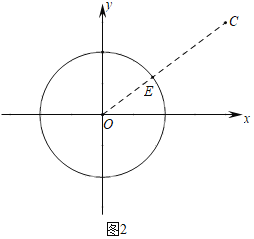
��C��4��3����
��OC��![]() ��5��
��5��
��OE��2��
��EC��3��
��d��T����O����3��
�ʴ�Ϊ3��
����ͼ����ֱ��y��kx+![]() ��y��Ľ���ΪD�����O������E��K������OK��OE��
��y��Ľ���ΪD�����O������E��K������OK��OE��
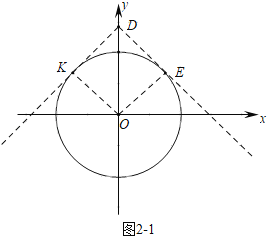
��OE��DE��OK��DK��OD��![]() ��OE��OK��2��
��OE��OK��2��
��DK��![]() ��2��DE��
��2��DE��![]() ��2��
��2��
��DE��OE��DK��OK��
���ı���DEOK�����Σ�
�ߡ�DKO����DEO��90����
���ı���DEOK�������Σ�
���ODE����ODK��45����
��ֱ��DE�Ľ���ʽΪy����x+![]() ��ֱ��DK�Ľ���ʽΪy��x+
��ֱ��DK�Ľ���ʽΪy��x+![]() ��
��
��d��T����O��0��
��۲�ͼ���֪����������k��ֵΪ��1��k��1��k��0��
��3����ͼ3��1�У�����P�ڡ�DOE�ڲ�ʱ����PM��OD��M������P��K��
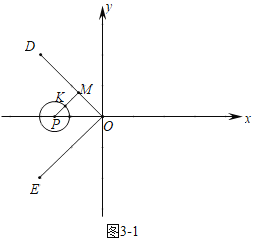
��D����8��8����
���DOP��45����
��d��T����P����1��
��PM��OM��3��OP��![]() ��
��
��t����![]() ��
��
��ͼ3��2�У�����P�ڡ�DOE�����ʱ���������֪OM��1��OP��1+2��3��t��3��
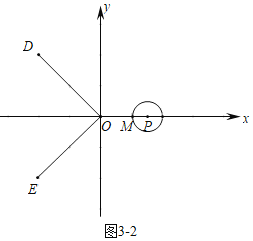
��������������������t��ֵΪ��![]() ��3��
��3��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��ֱ֪��y=-2x+3��������y=x2�ཻ��A,B����,OΪ����ԭ��.
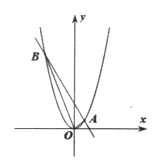
(1)���A��B�����ꣻ
(2)����OA,OB,���OAB�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����ⷢ��
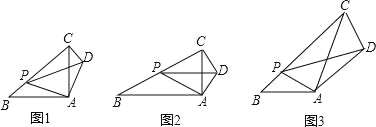
��ͼ1����Rt��ABC�У���A=90�㣬![]() =1����P�DZ�BC��һ���㣨�����B�غϣ�����PAD=90�㣬��APD=��B������ CD��
=1����P�DZ�BC��һ���㣨�����B�غϣ�����PAD=90�㣬��APD=��B������ CD��
��1������![]() ��ֵ�������ACD�Ķ�����
��ֵ�������ACD�Ķ�����
��2����չ̽��
��ͼ 2����Rt��ABC�У���A=90�㣬![]() =k����P�DZ�BC��һ���㣨�����B�غϣ�����PAD=90�㣬��APD=��B������CD�����жϡ�ACD���B ��������ϵ�Լ�PB��CD֮���������ϵ����˵�����ɣ�
=k����P�DZ�BC��һ���㣨�����B�غϣ�����PAD=90�㣬��APD=��B������CD�����жϡ�ACD���B ��������ϵ�Լ�PB��CD֮���������ϵ����˵�����ɣ�
��3���������
��ͼ 3���ڡ�ABC�У���B=45�㣬AB=4![]() ��BC=12��P �DZ�BC��һ���㣨�����B�غϣ�����PAD=��BAC����APD=��B������CD���� PA=5����ֱ��д��CD�ij���
��BC=12��P �DZ�BC��һ���㣨�����B�غϣ�����PAD=��BAC����APD=��B������CD���� PA=5����ֱ��д��CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
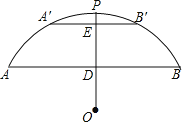
����Ŀ����ͼ����һ��������Բ���Σ����Ŀ��AB=60�ף�����PD=18�ף�
��1����Բ�����ڵ�Բ�İ뾶r�ij���
��2������ˮ���ĵ����ֻ��30��ʱ��Ҫ��ȡ������ʩ����������ˮ��ֻ��4�ף���PE=4��ʱ���Ƿ�Ҫ��ȡ������ʩ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������4�����⣺��������������Ի�һ��Բ����ͬԲ���ڽ������κ��ڽ��������εı߳�����![]() ��
��![]() ���������ε����ĵ������ε����߾�����ȣ���������ȵĻ��ǵȻ���������ȷ����_____������ţ���
���������ε����ĵ������ε����߾�����ȣ���������ȵĻ��ǵȻ���������ȷ����_____������ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=x+2��������y=ax2+bx+6��a��0���ཻ��A��![]() ��
��![]() ����B��4��m������P���߶�AB������A��B�Ķ��㣬����P��PC��x���ڵ�D�����������ڵ�C��
����B��4��m������P���߶�AB������A��B�Ķ��㣬����P��PC��x���ڵ�D�����������ڵ�C��
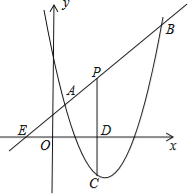
��1���������ߵĽ���ʽ��
��2���Ƿ����������P�㣬ʹ�߶�PC�ij������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�
��3����PACΪֱ��������ʱ��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2��bx��c��a��0����ͼ����ʾ���Գ���Ϊx��1���������н��ۣ���abc��0���ڵ�x��2ʱ��y��0����3a��c��0����3a+b��0��������ȷ�Ľ����У� ��

A. �٢� B. �٢� C. �٢ۢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����IJ��ϣ��ش����⣺
�ⷽ��![]() ������һ��һԪ�Ĵη��̣����ݸ÷��̵��ص㣬���Ľⷨͨ���ǣ���
������һ��һԪ�Ĵη��̣����ݸ÷��̵��ص㣬���Ľⷨͨ���ǣ���![]() ����ô
����ô![]() ������ԭ���̿ɱ�Ϊ
������ԭ���̿ɱ�Ϊ![]() �٣����
�٣����![]() ��
��![]() .
.
��![]() ʱ��
ʱ��![]() ����
����![]()
��![]() ʱ��
ʱ��![]() ����
����![]()
��ԭ�������ĸ�����![]() ��
��![]() ��
��![]() ��
��![]() .
.
��1������ԭ���̵õ����̢ٵĹ����У�����________���ﵽ________��Ŀ�ģ���������ѧ��ת��˼��.
��2���ⷽ��![]() .
.
��3����֪����ʵ��a��b����![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ͬһƽ��ֱ������ϵ�У����κ���y��ax2��bx��c����κ���y��(a��3)x2��(b��15)x��c��18��ͼ����x��Ľ���ֱ���A��B��C��
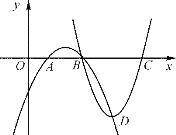
(1)�ж�ͼ�о�����B��D��C��ͼ������һ�����κ�����ͼ����˵�����ɣ�
(2)������������ͼ������B��D�����B��D�ĺ����꣮
(3)����D�ǹ���B��D��C�ĺ���ͼ��Ķ��㣬������Ϊ��2���������������Ľ���ʽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com