
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(![]() ,
,![]() )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
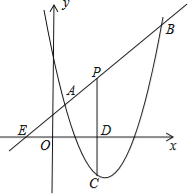
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值,若存在,求出这个最大值;若不存在,请说明理由;
(3)求PAC为直角三角形时点P的坐标.
【答案】解:(1)∵B(4,m)在直线y=x+2上
∴m=6,即B(4,6)
∵A![]() 和B(4,6)在抛物线
和B(4,6)在抛物线![]() 上
上
∴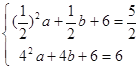
解得![]()
∴抛物线的解析式![]() ;
;
(2)存在.
设动点P的坐标为(n,n+2),点C的坐标为(n,2n2-8n+6),
∴PC=(n+2)-(2n2-8n+6),
=-2n2+9n-4,
=-2(n-![]() )+
)+![]()
∵-2<0,
∴当n=![]() 时,线段PC最大且为
时,线段PC最大且为![]() .
.
【解析】试题分析:(1)已知B(4,m)在直线y=x+2上,可求得m的值,抛物线图象上的A、B两点坐标,可将其代入抛物线的解析式中,通过联立方程组即可求得待定系数的值.
(2)要弄清PC的长,实际是直线AB与抛物线函数值的差.可设出P点横坐标,根据直线AB和抛物线的解析式表示出P、C的纵坐标,进而得到关于PC与P点横坐标的函数关系式,根据函数的性质即可求出PC的最大值.
(3)当△PAC为直角三角形时,根据直角顶点的不同,有三种情形,需要分类讨论,分别求解.
试题解析:(1)∵B(4,m)在直线y=x+2上,
∴m=4+2=6,
∴B(4,6),
∵A(![]() ,
, ![]() )、B(4,6)在抛物线y=
)、B(4,6)在抛物线y= ![]() +bx+6上,
+bx+6上,
∴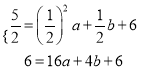 ,解得
,解得![]() ,
,
∴抛物线的解析式为y=![]() ﹣8x+6;
﹣8x+6;
(2)设动点P的坐标为(n,n+2),则C点的坐标为(n, ![]() ﹣8n+6),
﹣8n+6),
∴PC=(n+2)﹣(![]() ﹣8n+6),
﹣8n+6),
=﹣![]() +9n﹣4,
+9n﹣4,
=![]() ,
,
∵PC>0,
∴当n=![]() 时,线段PC最大值为
时,线段PC最大值为![]() ;
;
(3)∵△PAC为直角三角形,
i)若点P为直角顶点,则∠APC=90°.
由题意易知,PC∥y轴,∠APC=45°,因此这种情形不存在;
ii)若点A为直角顶点,则∠PAC=90°.
如答图3﹣1,过点A(![]() ,
, ![]() )作AN⊥x轴于点N,则ON=
)作AN⊥x轴于点N,则ON=![]() ,AN=
,AN=![]() .
.
过点A作AM⊥直线AB,交x轴于点M,则由题意易知,△AMN为等腰直角三角形,
∴MN=AN=![]() ,∴OM=ON+MN=
,∴OM=ON+MN=![]() +
+![]() =3,
=3,
∴M(3,0).
设直线AM的解析式为:y=kx+b,
则: 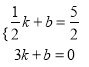 ,解得
,解得![]() ,
,
∴直线AM的解析式为:y=﹣x+3①,
又抛物线的解析式为:y=![]() ﹣8x+6②,
﹣8x+6②,
联立①②式,解得:x=3或x=![]() (与点A重合,舍去),
(与点A重合,舍去),
∴C(3,0),即点C、M点重合.
当x=3时,y=x+2=5,
∴![]() (3,5);
(3,5);
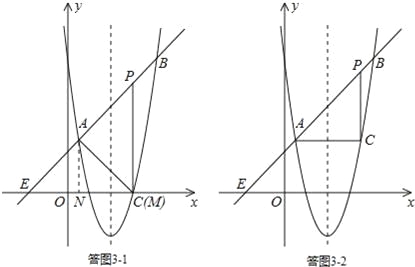
iii)若点C为直角顶点,则∠ACP=90°.
∵y=![]() ﹣8x+6=
﹣8x+6=![]() ,
,
∴抛物线的对称轴为直线x=2.
如答图3﹣2,作点A(![]() ,
, ![]() )关于对称轴x=2的对称点C,
)关于对称轴x=2的对称点C,
则点C在抛物线上,且C(![]() ,
, ![]() ).
).
当x=![]() 时,y=x+2=
时,y=x+2=![]() .
.
∴![]() (
(![]() ,
, ![]() ).
).
∵点![]() (3,5)、
(3,5)、![]() (
(![]() ,
, ![]() )均在线段AB上,
)均在线段AB上,
∴综上所述,△PAC为直角三角形时,点P的坐标为(3,5)或(![]() ,
, ![]() ).
).


科目:初中数学 来源: 题型:
【题目】二次函数的图象经过A(1,m),B(2,n),C(4,t),且点B是该二次函数图象的顶点.
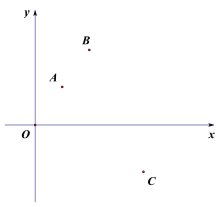
(1)若m=3,n=4,求二次函数解析式;
(2)请在图中描出该函数图象上另外的两个点,并画出图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车租赁公司共有汽车50辆,市场调查表明,当租金为每辆每日200元时可全部租出,当租金每提高10元,租出去的车就减少2辆.
(1)当租金提高多少元时,公司的每日收益可达到10120元?
(2)汽车日常维护要一定费用,已知外租车辆每日维护费为100元,未租出的车辆维护费为50元,当租金为多少元时,公司的利润恰好为5500元?(利润=收益-维护费)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为1,△ABC是⊙O的内接等边三角形,点D,E在圆上,四边形BCDE为矩形,这个矩形的面积是( )

A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】概念认识
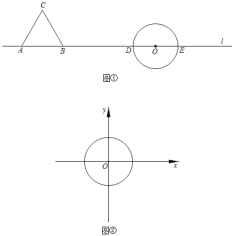
平面内,M为图形T上任意一点,N为⊙O上任意一点,将M、N两点间距离的最小值称为图形T到⊙O的“最近距离”,记作d(T﹣⊙O).例如图①,在直线l上有A、B、O三点,以AB为一边作等边△ABC,以点O为圆心作圆,与l交于D、E两点,若将△ABC记为图形T,则B、D两点间的距离称为图形T到⊙O的“最近距离”.
数学理解
(1)在直线l上有A、B两点,以点A为圆心,3为半径作⊙A,将点B记为图形T,若d(T﹣⊙A)=1,则AB= .
(2)如图②,在平面直角坐标系中,以O(0,0)为圆心,半径为2作圆.
①将点C(4,3)记为图形T,则d(T﹣⊙O)= .
②将一次函数y=kx+2![]() 的图记为图形T,若d(T﹣⊙O)>0,求k的取值范围.
的图记为图形T,若d(T﹣⊙O)>0,求k的取值范围.
推广运用
(3)在平面直角坐标系中,P的坐标为(t,0),⊙P的半径为2,D、E两点的坐标分别为(﹣8,8)、(﹣8,﹣8),将∠DOE记为图形T,若d(T﹣⊙P)=1,则t= .
查看答案和解析>>
科目:初中数学 来源: 题型:
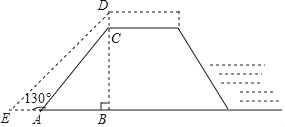
【题目】为做好防汛工作,防汛指挥部决定对某水库的水坝进行加高加固,专家提供的方案是:水坝加高2米(即CD=2米),背水坡DE的坡度i=1:1(即DB:EB=1:1),如图所示,已知AE=4米,∠EAC=130°,求水坝原来的高度BC.(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县某中学开展“庆十一”爱国知识竞赛活动,九年级(1)、(2)班各选出![]() 名选手参加比赛,两个班选出的
名选手参加比赛,两个班选出的![]() 名选手的比赛成绩(满分为100分)如图所示。
名选手的比赛成绩(满分为100分)如图所示。

(1)根据图示填写如表:
班级 | 中位数(分) | 众数(分) |
九(1) |
| 85 |
九(2) | 80 |
|
(2)请你计算九(1)和九(2)班的平均成绩各是多少分。
(3)结合两班竞赛成绩的平均数和中位数,分析哪个班级的竞赛成绩较好
(4)请计算九(1)、九(2)班的竞赛成绩的方差,并说明哪个班的成绩比较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=﹣![]() (x>0)与y=
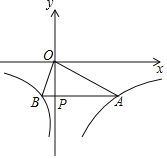
(x>0)与y=![]() (x<0)的图象如图所示,点P是y轴负半轴上一动点,过点P作y轴的垂线交图象于A、B两点,连接OA、OB.下列结论;①若点M1(x1,y1),M2(x2,y2)在图象上,且x1<x2<0,则y1<y2;②当点P坐标为(0,﹣3)时,△AOB是等腰三角形;③无论点P在什么位置,始终有S△AOB=7.5,AP=4BP;④当点P移动到使∠AOB=90°时,点A的坐标为(2
(x<0)的图象如图所示,点P是y轴负半轴上一动点,过点P作y轴的垂线交图象于A、B两点,连接OA、OB.下列结论;①若点M1(x1,y1),M2(x2,y2)在图象上,且x1<x2<0,则y1<y2;②当点P坐标为(0,﹣3)时,△AOB是等腰三角形;③无论点P在什么位置,始终有S△AOB=7.5,AP=4BP;④当点P移动到使∠AOB=90°时,点A的坐标为(2![]() ,﹣
,﹣![]() ).其中正确的结论为___.
).其中正确的结论为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,(n+1)个边长为2的等边三角形有一条边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△B(n+1)DnCn的面积为Sn,则Sn=____(用含n的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com