
����Ŀ����֪����y����![]() ��x��0����y��
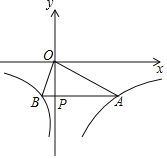
��x��0����y��![]() ��x��0����ͼ����ͼ��ʾ����P��y�Ḻ������һ���㣬����P��y��Ĵ��߽�ͼ����A��B���㣬����OA��OB�����н��ۣ�������M1��x1��y1����M2��x2��y2����ͼ���ϣ���x1��x2��0����y1��y2���ڵ���P����Ϊ��0����3��ʱ����AOB�ǵ��������Σ������۵�P��ʲôλ�ã�ʼ����S��AOB��7.5��AP��4BP���ܵ���P�ƶ���ʹ��AOB��90��ʱ����A������Ϊ��2
��x��0����ͼ����ͼ��ʾ����P��y�Ḻ������һ���㣬����P��y��Ĵ��߽�ͼ����A��B���㣬����OA��OB�����н��ۣ�������M1��x1��y1����M2��x2��y2����ͼ���ϣ���x1��x2��0����y1��y2���ڵ���P����Ϊ��0����3��ʱ����AOB�ǵ��������Σ������۵�P��ʲôλ�ã�ʼ����S��AOB��7.5��AP��4BP���ܵ���P�ƶ���ʹ��AOB��90��ʱ����A������Ϊ��2![]() ����
����![]() ����������ȷ�Ľ���Ϊ___��
����������ȷ�Ľ���Ϊ___��
���𰸡��ڢۢܣ�
��������
�ٴ�����x1��x2��0ʱ������y��x���������С�ɵã�
����ȷ�����A��B�������꼴�ɽ�����⣻
����ȷ����P��0��m������B��![]() ��m����A����
��m����A����![]() ��m�������PA��PB���Ƴ�PA��4PB����SAOB��S��OPB+S��OPA�������S��AOB��7.5��
��m�������PA��PB���Ƴ�PA��4PB����SAOB��S��OPB+S��OPA�������S��AOB��7.5��
����ȷ����P��0��m������B��![]() ��m����A����
��m����A����![]() ��m�����Ƴ�PB����
��m�����Ƴ�PB����![]() ��PA����
��PA����![]() ��OP����m���ɡ�OPB�ס�APO���ɵ�OP2��PBPA���г����̼��ɽ�����⣮
��OP����m���ɡ�OPB�ס�APO���ɵ�OP2��PBPA���г����̼��ɽ�����⣮
�⣺�ٴ���x1��x2��0������y��x���������С��
��y1��y2���ʢٴ���
����ȷ����P��0����3����
��B����1����3����A��4����3����
��AB��5��OA��![]() ��5��
��5��
��AB��AO��
���AOB�ǵ��������Σ��ʢ���ȷ��
����ȷ����P��0��m������B��![]() ��m����A����
��m����A����![]() ��m����
��m����
��PB����![]() ��PA����
��PA����![]() ��
��
��PA��4PB��
��SAOB��S��OPB+S��OPA��![]() +
+![]() ��7.5���ʢ���ȷ��
��7.5���ʢ���ȷ��
����ȷ����P��0��m������B��![]() ��m����A����
��m����A����![]() ��m����
��m����
��PB����![]() ��PA����
��PA����![]() ��OP����m��
��OP����m��
�ߡ�AOB��90������OPB����OPA��90����
���BOP+��AOP��90������AOP+��OAP��90����
���BOP����OAP��
���OPB�ס�APO��
��![]() ��
��![]() ��
��
��OP2��PBPA��
��m2����![]() ����
����![]() ����
����
��m4��36��
��m��0��
��m����![]() ��
��
��A��2![]() ����
����![]() �����ʢ���ȷ��
�����ʢ���ȷ��
��ڢۢ���ȷ��
�ʴ�Ϊ���ڢۢܣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
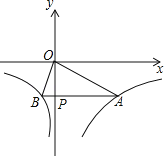
����Ŀ����ͼ����ABC���CDEΪ����ֱ�������Σ���BAC=��DEC=90�㣬����AD��ȡAD�е�P������BP�����ӳ�����M��ʹBP=PM������AM��EM��AE������CDE�Ƶ�C˳ʱ����ת��
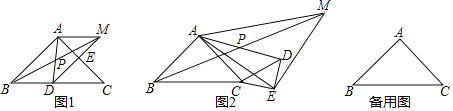
��1����ͼ�٣�����D��BC�ϣ�E��AC��ʱ��AE��AM��������ϵ��______����MAE=______��
��2������CDE�Ƶ�C˳ʱ����ת����ͼ����ʾ��λ�ã���1���еĽ����Ƿ���Ȼ�������������������֤����������������˵�����ɣ�
��3����CD=![]() BC������CDE��ͼ��λ���Ƶ�C˳ʱ����ת����0�㣼����360�㣩����ME=
BC������CDE��ͼ��λ���Ƶ�C˳ʱ����ת����0�㣼����360�㣩����ME=![]() CDʱ����ֱ��д������ֵ��
CDʱ����ֱ��д������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=x+2��������y=ax2+bx+6��a��0���ཻ��A��![]() ��
��![]() ����B��4��m������P���߶�AB������A��B�Ķ��㣬����P��PC��x���ڵ�D�����������ڵ�C��
����B��4��m������P���߶�AB������A��B�Ķ��㣬����P��PC��x���ڵ�D�����������ڵ�C��
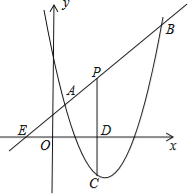
��1���������ߵĽ���ʽ��
��2���Ƿ����������P�㣬ʹ�߶�PC�ij������ֵ�������ڣ����������ֵ���������ڣ���˵�����ɣ�
��3����PACΪֱ��������ʱ��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
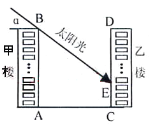
����Ŀ����ͼΪijС��������1O��סլ¥���ɵ�����������Ϊ��1�㡢��2�㡢������10�㣬ÿ��ĸ߶�Ϊ3m����¥��ľ���AC=30m�������˽���ijһʱ���ڣ���¥����¥�IJɹ��Ӱ�����������ijһʱ�̼�¥¥��B������¥��Ӱ�ӳ�EC=h��̫��������ˮƽ�ߵļн�Ϊ����
(1)�ú�����ʽ�ӱ�ʾh��
(2)������30��ʱ����¥¥��B��Ӱ��������¥�ĵڼ���?�Ӵ�ʱ��������ÿСʱ����10�㣬��Сʱ��¥��Ӱ�Ӹպò�Ӱ����¥�ɹ⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����IJ��ϣ��ش����⣺
�ⷽ��![]() ������һ��һԪ�Ĵη��̣����ݸ÷��̵��ص㣬���Ľⷨͨ���ǣ���
������һ��һԪ�Ĵη��̣����ݸ÷��̵��ص㣬���Ľⷨͨ���ǣ���![]() ����ô
����ô![]() ������ԭ���̿ɱ�Ϊ
������ԭ���̿ɱ�Ϊ![]() �٣����
�٣����![]() ��
��![]() .
.
��![]() ʱ��
ʱ��![]() ����
����![]()
��![]() ʱ��
ʱ��![]() ����
����![]()
��ԭ�������ĸ�����![]() ��
��![]() ��
��![]() ��
��![]() .
.
��1������ԭ���̵õ����̢ٵĹ����У�����________���ﵽ________��Ŀ�ģ���������ѧ��ת��˼��.
��2���ⷽ��![]() .
.
��3����֪����ʵ��a��b����![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣��ھ���OABC�У�OA��4��OC��3���ֱ���OC��OA���ڵ�ֱ��Ϊx�ᡢy�ᣬ������ͼ��ʾ������ϵ������OB������������y��![]() ��x��0����ͼ���߶�OB���е�D��������ε����߽��ڵ�E�͵�F��ֱ��l��y��kx+b������E�͵�F��
��x��0����ͼ���߶�OB���е�D��������ε����߽��ڵ�E�͵�F��ֱ��l��y��kx+b������E�͵�F��
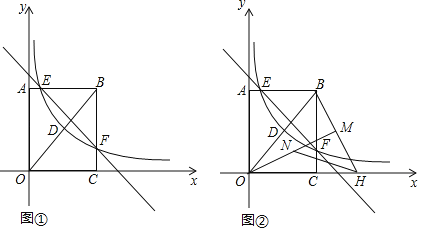
��1�����������Ľ���ʽ��
��2������OE��OF������OEF�������
��3���ڵ�һ�����ڣ���ֱ��д������x�IJ���ʽkx+b��![]() �Ľ⼯���� ��
�Ľ⼯���� ��
��4����ͼ�ڣ����߶�OB�Ƶ�O˳ʱ����תһ���Ƕȣ�ʹ�õ�B�Ķ�Ӧ��Hǡ������x����������ϣ�����BH����OM��BH����NΪ�߶�OM�ϵ�һ�����㣬��HN+![]() ON����Сֵ��
ON����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ijУ��ʵ�¿θľ������r�����Ը�Уij���ͬѧ�μӿ��������Ϊ����������μ������������滭�������赸�������������������������������е���ͳ�ƣ�����������ͼ��ʾ��ͳ��ͼ��
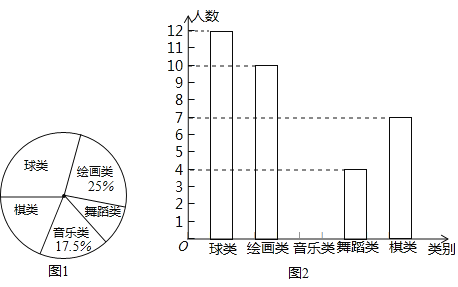
��1���μ���������ѧ������Ϊ�� �ˣ��μ������������İٷֱ�Ϊ�� ��
��2���������ͳ��ͼ����������
��3������Уѧ����1600�ˣ���ô�������Ĵ�Լ�ж����ˣ�
��4���ð�μ��赸��4λͬѧ�У���1λ��������E��ʾ����3λŮ�����ֱ�F��G��H��ʾ������������ѡȡ����ͬѧ�����飬�����б�����״�ķ�����ǡ��ѡ��һ��һŮ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У���ABC=90������BAC��30��������ABC�Ƶ�A˳ʱ����תһ���ĽǶ�![]() �õ���AED����B��C�Ķ�Ӧ��ֱ���E��D.
�õ���AED����B��C�Ķ�Ӧ��ֱ���E��D.
(1)��ͼ1������Eǡ����AC��ʱ�����CDE�Ķ�����
(2)��ͼ2����![]() =60��ʱ����F�DZ�AC�е㣬��֤���ı���BFDE��ƽ���ı���.
=60��ʱ����F�DZ�AC�е㣬��֤���ı���BFDE��ƽ���ı���.


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
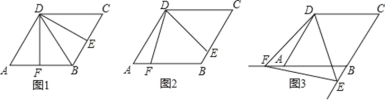
����Ŀ����ͼ���ı��� ABCD �DZ߳�Ϊ 2��һ����ǵ��� 60��������ֽƬ����һ����EDF=60����������ֽƬ��һ������������ζ��� D �غϣ���˳ʱ�뷽����ת���������ֽƬ��ʹ�������߷ֱ� CB��BA�������ǵ��ӳ������ڵ� E�� F��
�ٵ� CE=AF ʱ����ͼ����DE �� DF ��������ϵ�� ��
�ڼ�����ת������ֽƬ���� CE��AF ʱ����ͼ������1���Ľ����Ƿ������������������֤����������������˵�����ɣ�
���ٴ���ת������ֽƬ������ E��F �ֱ��� CB��BA ���ӳ�����ʱ����ͼ���� ��ֱ��д�� DE �� DF ��������ϵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com