
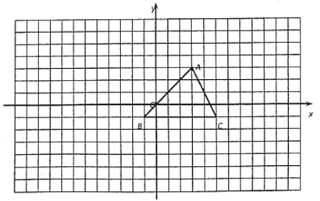
����Ŀ����ͼ�٣��ھ���OABC�У�OA��4��OC��3���ֱ���OC��OA���ڵ�ֱ��Ϊx�ᡢy�ᣬ������ͼ��ʾ������ϵ������OB������������y��![]() ��x��0����ͼ���߶�OB���е�D��������ε����߽��ڵ�E�͵�F��ֱ��l��y��kx+b������E�͵�F��
��x��0����ͼ���߶�OB���е�D��������ε����߽��ڵ�E�͵�F��ֱ��l��y��kx+b������E�͵�F��
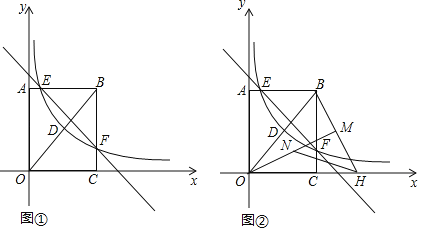
��1�����������Ľ���ʽ��
��2������OE��OF������OEF�������
��3���ڵ�һ�����ڣ���ֱ��д������x�IJ���ʽkx+b��![]() �Ľ⼯���� ��
�Ľ⼯���� ��
��4����ͼ�ڣ����߶�OB�Ƶ�O˳ʱ����תһ���Ƕȣ�ʹ�õ�B�Ķ�Ӧ��Hǡ������x����������ϣ�����BH����OM��BH����NΪ�߶�OM�ϵ�һ�����㣬��HN+![]() ON����Сֵ��
ON����Сֵ��
���𰸡���1��y��![]() ����2��S��OEF��
����2��S��OEF��![]() ����3��0��x��
����3��0��x��![]() ��x��3����4��HN+
��x��3����4��HN+![]() ON����СֵΪ4��
ON����СֵΪ4��
��������
��1������ȷ����B���꣬�ٸ����е����깫ʽ�����D�����꼴�ɽ�����⣮
��2�������E��F�����꣬�ٸ���S��OEF=S����ABCO-S��AOE-S��OCF-S��EFB���㼴�ɣ�
��3��д���ڵ�һ���ޣ�ֱ�ߵ�ͼ���ڷ�����������ͼ����·����Ա���x��ȡֵ��Χ���ɣ�
��4����ͼ���У���NJ��BD��J��HK��BD��K����ֱ������������֤����sin��NOD=![]() ���Ƴ�NJ=ONsin��NOD=
���Ƴ�NJ=ONsin��NOD=![]() ON���Ƴ�NH+
ON���Ƴ�NH+![]() ON=NH+NJ�����ݴ��߶���̿�֪����J��N��H���ߣ�����HK�غ�ʱ��HN+
ON=NH+NJ�����ݴ��߶���̿�֪����J��N��H���ߣ�����HK�غ�ʱ��HN+![]() ON��ֵ��С����Сֵ=HK�ij����ɴ˼��ɽ�����⣮
ON��ֵ��С����Сֵ=HK�ij����ɴ˼��ɽ�����⣮
�⣺��1���ھ���ABCO�У���OA��BC��4��OC��AB��3��
��B��3��4����
��OD��DB��
��D��![]() ��2����
��2����
��y��![]() ����D��
����D��![]() ��2����
��2����
��k��3��
�෴���������Ľ���ʽΪy��![]() ��
��
��2����ͼ���У�����OE��OF��
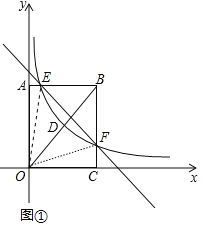
������E��![]() ��4����F��3��1����
��4����F��3��1����
��S��OEF��S����ABCO��S��AOE��S��OCF��S��EFB
��12��![]() ��4��
��4��![]() ��
��![]() ��3��1��
��3��1��![]() ��3����3��
��3����3��![]() ��
��
��![]() ��
��
��3���۲�ͼ���֪���ڵ�һ�����ڣ�����x�IJ���ʽkx+b��![]() �Ľ⼯Ϊ��0��x��
�Ľ⼯Ϊ��0��x��![]() ��x��3��
��x��3��
�ʴ�Ϊ��0��x��![]() ��x��3��
��x��3��
��4����ͼ���У���NJ��BD��J��HK��BD��K��
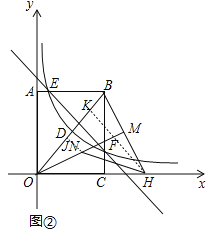
������OB��OH��5��
��CH��OH��OC��5��3��2��
��BH��![]() ��
��![]() ��2
��2![]() ��
��
��sin��CBH��![]() ��
��![]() ��
��
��OM��BH��
���OMH����BCH��90����
�ߡ�MOH+��OHM��90������CBH+��CHB��90����
���MOH����CBH��
��OB��OH��OM��BH��
���MOB����MOH����CBH��
��sin��NOD��![]() ��
��
��NJ��ONsin��NOD��![]() ON��
ON��
��NH+![]() ON��NH+NJ��
ON��NH+NJ��
���ݴ��߶���̿�֪����J��N��H���ߣ�����HK�غ�ʱ��HN+![]() ON��ֵ��С����Сֵ��HK�ij���
ON��ֵ��С����Сֵ��HK�ij���
��OB��OH��BC��OH��HK��OB��
��HK��BC��4��
��HN+![]() ON����СֵΪ4��
ON����СֵΪ4��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������˾��������50�����г���������������Ϊÿ��ÿ��200Ԫʱ��ȫ������������ÿ���10Ԫ�����ȥ�ij��ͼ���2����
��1���������߶���Ԫʱ����˾��ÿ������ɴﵽ10120Ԫ��
��2����˾�쵼ϣ��������ﵽ10200Ԫ������Ϊ�ܷ�ʵ�֣����ܣ������ʱ����������ܣ���˵�����ɣ�
��3�������ճ�ά��Ҫһ�����ã���֪�����ÿ��ά����Ϊ100Ԫ��δ����ij���ά����Ϊ50Ԫ�������Ϊ����Ԫʱ����˾������ǡ��Ϊ5500Ԫ������������һά���ѣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���÷�Ѵ��������Ѵָ�Ӳ�������ijˮ���ˮ�ӽ��мӸӹ̣�ר���ṩ�ķ����ǣ�ˮ�ӼӸ�2�ף���CD=2�ף�����ˮ��DE���¶�i=1��1����DB��EB=1��1������ͼ��ʾ����֪AE=4�ף���EAC=130������ˮ��ԭ���ĸ߶�BC�����ο����ݣ�sin50���0.77��cos50���0.64��tan50���1.2��
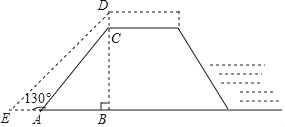
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() ��
��![]() ��
��![]() .
.
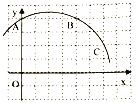
��1������A��B��C�����Բ������Բ��Բ��M������Ϊ________.
��2����D����Ϊ![]() ������CD���ж�ֱ��CD���M��λ�ù�ϵ��˵������.
������CD���ж�ֱ��CD���M��λ�ù�ϵ��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y����![]() ��x��0����y��
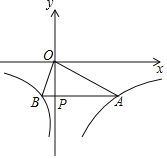
��x��0����y��![]() ��x��0����ͼ����ͼ��ʾ����P��y�Ḻ������һ���㣬����P��y��Ĵ��߽�ͼ����A��B���㣬����OA��OB�����н��ۣ�������M1��x1��y1����M2��x2��y2����ͼ���ϣ���x1��x2��0����y1��y2���ڵ���P����Ϊ��0����3��ʱ����AOB�ǵ��������Σ������۵�P��ʲôλ�ã�ʼ����S��AOB��7.5��AP��4BP���ܵ���P�ƶ���ʹ��AOB��90��ʱ����A������Ϊ��2
��x��0����ͼ����ͼ��ʾ����P��y�Ḻ������һ���㣬����P��y��Ĵ��߽�ͼ����A��B���㣬����OA��OB�����н��ۣ�������M1��x1��y1����M2��x2��y2����ͼ���ϣ���x1��x2��0����y1��y2���ڵ���P����Ϊ��0����3��ʱ����AOB�ǵ��������Σ������۵�P��ʲôλ�ã�ʼ����S��AOB��7.5��AP��4BP���ܵ���P�ƶ���ʹ��AOB��90��ʱ����A������Ϊ��2![]() ����
����![]() ����������ȷ�Ľ���Ϊ___��
����������ȷ�Ľ���Ϊ___��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
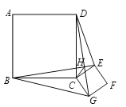
����Ŀ����ͼ��������ABCD��������CEFG�ı߳��ֱ�Ϊa��b��BE��DG�ཻ�ڵ�H������HC���������н��ۣ���BE=DG����BE��DG����DE2+BG2=2a2+2b2��������ȷ�Ľ�����__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
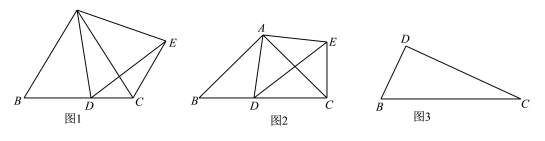
����Ŀ����ͼ1������ABC�У�AB=AC����BAC=60����DΪBC����һ�㣬(�����B��C)�غϣ����߶�AD�Ƶ�A��ʱ����ת60���õ�AE������EC�����ACE�Ķ�����__________���߶�AC��CD��CE֮���������ϵ��_______________.
(2)2������ABC�У�AB=AC����BAC=90����DΪBC����һ��(�����B��C�غ�)�����߶�AD�Ƶ�A��ʱ����ת90���õ�AE������EC����д����ACE�Ķ������߶�AD��BD��CD֮���������ϵ����˵������.
(3)��ͼ3����Rt��DBC�У�DB=3��DC=5����BDC=90��������A����AB=AC����BAC=90������ֱ��д���߶�AD�ij���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һֻ�����Ĵ����У�װ��2������1������1��������Щ�����ɫ�ⶼ��ͬ�������б���������ͼ���������¼��ĸ��ʣ�
(1)���Ⱥ������������1����ǡ���ǰ���
(2)���Ⱥ������������2����2�����ǰ���
(3)�ٷ��뼸������ɫ�ⶼ��ͬ�ĺ����Ⱥ������������1����ǡ���Ǻ���ĸ���Ϊ![]() ��������˼�������
��������˼�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1�������Σ����ǰ��Ը�������Ϊ�ߵ������γ�Ϊ��������Σ�ͼ�е�![]() ���Ǹ��������.�ڽ���ƽ��ֱ������ϵ��
���Ǹ��������.�ڽ���ƽ��ֱ������ϵ��![]() ������Ϊ
������Ϊ![]() .
.
��1����![]() ����ƽ��8���õ�
����ƽ��8���õ�![]() ��������ϵ����ֽ�л���
��������ϵ����ֽ�л���![]() ��ͼ�β�ֱ��д����
��ͼ�β�ֱ��д����![]() ������Ϊ____��
������Ϊ____��
��2����![]() �Ƶ�
�Ƶ�![]() ��˳ʱ�뷽����ת
��˳ʱ�뷽����ת![]() ��õ�
��õ�![]() ��������ϵ����ֽ�л���
��������ϵ����ֽ�л���![]() ��ͼ�β�ֱ��д����
��ͼ�β�ֱ��д����![]() ������Ϊ____________��
������Ϊ____________��
��3������������ϵ�ķ���ֽ����![]() �Ե�
�Ե�![]() Ϊλ�����ķŴ�ʹ�Ŵ�ǰ���Ӧ�߳��ı�Ϊ
Ϊλ�����ķŴ�ʹ�Ŵ�ǰ���Ӧ�߳��ı�Ϊ![]() ������
������![]() .
.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com