
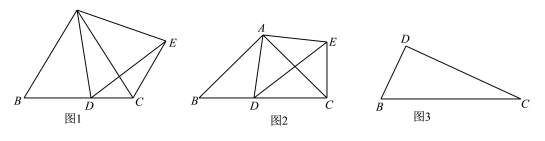
【题目】如图1,在△ABC中,AB=AC,∠BAC=60°,D为BC边上一点,(不与点B、C)重合,将线段AD绕点A逆时针旋转60°得到AE,连接EC,则∠ACE的度数是__________,线段AC,CD,CE之间的数量关系是_______________.
(2)2,在△ABC中,AB=AC,∠BAC=90°,D为BC边上一点(不与点B、C重合),将线段AD绕点A逆时针旋转90°得到AE,连接EC,请写出∠ACE的度数及线段AD,BD,CD之间的数量关系,并说明理由.
(3)如图3,在Rt△DBC中,DB=3,DC=5,∠BDC=90°,若点A满足AB=AC,∠BAC=90°,请直接写出线段AD的长度.
【答案】(1)60°,AC=DC+EC(2)∠ACE=45°,BD2+CD2=2AD2,详见解析(3)AD=![]() 或AD=
或AD=![]()
【解析】
(1)证明△BAD≌△CAE,根据全等三角形的性质解答;
(2)根据全等三角形的性质得到BD=CE,∠ACE=∠B,得到∠DCE=90°,根据勾股定理计算即可;
(3)如图3,作AE⊥CD于E,连接AD,根据勾股定理得到BC=![]() =
=![]() ,推出点B,C,A,D四点共圆,根据圆周角定理得到∠ADE=45°,求得△ADE是等腰直角三角形,得到AE=DE,根据勾股定理即可得到结论.
,推出点B,C,A,D四点共圆,根据圆周角定理得到∠ADE=45°,求得△ADE是等腰直角三角形,得到AE=DE,根据勾股定理即可得到结论.
(1)∵在△ABC中,AB=AC,∠BAC=60°,
∴∠BAC=∠DAE=60°,
∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE,
在△BAD和△CAE中,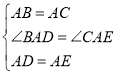 ,
,
∴△BAD≌△CAE(SAS),
∴∠ACE=∠B=60°,BD=CE,
∴BC=BD+CD=EC+CD,
∴AC=BC=EC+CD;
故答案为:60°,AC=DC+EC;
(2)BD2+CD2=2AD2,
理由如下:由(1)得,△BAD≌△CAE,∴BD=CE,∠ACE=∠B=45°,
∴∠DCE=90°,
∴CE2+CD2=ED2,
在Rt△ADE中,AD2+AE2=ED2,又AD=AE,
∴BD2+CD2=2AD2;
(3)如图3,作AE⊥CD于E,连接AD,
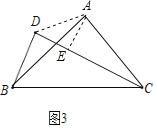
∵在Rt△DBC中,DB=3,DC=5,∠BDC=90°,
∴BC=![]() ,
,
∵∠BAC=90°,AB=AC,
∴AB=AC=![]() ,∠ABC=∠ACB=45°,
,∠ABC=∠ACB=45°,
∵∠BDC=∠BAC=90°,
∴点B,C,A,D四点共圆,
∴∠ADE=45°,
∴△ADE是等腰直角三角形,
∴AE=DE,
∴CE=5DE,
∵AE2+CE2=AC2,
∴AE2+(5AE)2=17,
∴AE=1,AE=4,
∴AD=![]() 或AD=
或AD=![]() .
.


科目:初中数学 来源: 题型:
【题目】某商店从机械厂购进甲、乙两种零件进行销售,若甲种零件每件的进价是乙种零件每件进价的![]() ,用1600元单独购进一种零件时,购进甲种零件的数量比乙种零件的数量多4件.
,用1600元单独购进一种零件时,购进甲种零件的数量比乙种零件的数量多4件.
(1)求每件甲种零件和每件乙种零件的进价分别为多少元?
(2)若该商店计划购进甲、乙两种零件共110件,准备将零件批发给零售商. 甲种零件的批发价是每件100元,乙种零件的批发价是每件130元,该商店计划将这批产品全部售出从零售商处获利不低于3000元,那么该商店最多购进多少件甲种零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与反比例函数
与反比例函数![]() 在第一象限内的图象交于点
在第一象限内的图象交于点![]() .
.
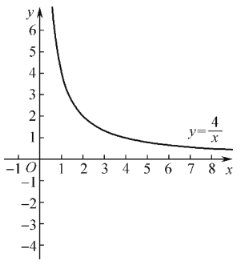
(1)求m、b的值;
(2)点B在反比例函数的图象上,且点B的横坐标为1.若在直线l上存在一点P(点P不与点A重合),使得![]() ,结合图象直接写出点P的横坐标
,结合图象直接写出点P的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
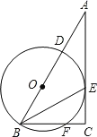
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.

(1)求证:直线DE是⊙O的切线;
(2)若⊙O半径为1,BC=4,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在 Rt△ABC 中,∠ACB=90°,BE 平分∠ABC,D 是边 AB 上一点,以 BD为直径的⊙O 经过点 E,且交 BC 于点 F.
(1)求证:AC 是⊙O 的切线;
(2)若 BC=8,⊙O 的半径为 5,求 CE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形![]() 的对角线
的对角线![]() 交点
交点![]() ,点
,点![]() 分别为边
分别为边![]() 的中点.有下列四个推断,
的中点.有下列四个推断,
①对于任意四边形![]() ,四边形
,四边形![]() 都是平行四边形;
都是平行四边形;
②若四边形![]() 是平行四边形,则
是平行四边形,则![]() 与
与![]() 交于点
交于点![]() ;
;
③若四边形![]() 是矩形,则四边形
是矩形,则四边形![]() 也是矩形;
也是矩形;
④若四边形![]() 是正方形,则四边形
是正方形,则四边形![]() 也一定是正方形.
也一定是正方形.
所有正确推断的序号是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,Rt△ABC中,∠C=90°,AB=15,BC=9,点D,E分别在AC,BC上,CD=4 x,CE=3x,其中0<x<3.
(1)求证:DE∥AB;
(2)当x=1时 ,求点E到AB的距离;
(3) 将△DCE绕点E逆时针方向旋转,使得点D落在AB边上的D′处. 在旋转的过程中,若点D′的位置有且只有一个,求x的取值范围.
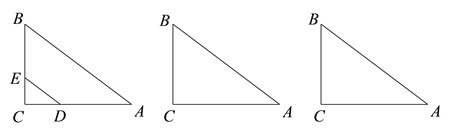
图1 备用图1 备用图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们“节能环保,绿色出行”意识的增强,越来越多的人喜欢骑自行车出行,也给自行车商家带来商机.某自行车行经营的A型自行车去年销售总额为8万元.今年该型自行车每辆售价预计比去年降低200元.若该型车的销售数量与去年相同,那么今年的销售总额将比去年减少10%,求:
(1)A型自行车去年每辆售价多少元?
(2)该车行今年计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的两倍.已知,A型车和B型车的进货价格分别为1500元和1800元,计划B型车销售价格为2400元,应如何组织进货才能使这批自行车销售获利最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com