【题目】某商店从机械厂购进甲、乙两种零件进行销售，若甲种零件每件的进价是乙种零件每件进价的
，用1600元单独购进一种零件时，购进甲种零件的数量比乙种零件的数量多4件.
（1）求每件甲种零件和每件乙种零件的进价分别为多少元?
（2）若该商店计划购进甲、乙两种零件共110件，准备将零件批发给零售商. 甲种零件的批发价是每件100元，乙种零件的批发价是每件130元，该商店计划将这批产品全部售出从零售商处获利不低于3000元，那么该商店最多购进多少件甲种零件?
【答案】（1）每件甲种零件的进价为80元，每件乙种零件的进价为100元.（2）该商店最多购进30件甲种零件
【解析】
（1）设甲种零件的单价为x元/件，则乙种零件的单价为0.8x元/件，根据等量关系：1600元购进的甲种零件的数量比1600元购进的乙种零件数量多4件列出方程，解方程即可得到所求答案；
（2）设购进甲种零件的数量为a件，则购进乙种零件的数量为（110-a）件，结合（1）中所得购进两种零件的单价和已知条件列出不等式，解不等式求得a的最大整数解，即可得到所求答案.
（1）设每件乙种零件的进价为x元，则每件甲种零件的进价为
元，由题意得：
解得x=100 ，
经检验x=100是所列方程的解，
∴=80.
答：每件甲种零件的进价为80元，每件乙种零件的进价为100元.
（2）设该商店购进甲a件甲种零件，根据题意可得：
≥3000，
解得a≤30，
∴a最大取30.
答：该商店最多购进30件甲种零件.
应用题作业本系列答案科目：初中数学 来源： 题型：
【题目】将5张都是10元的纸币随机装入10个完全相同的信封中，设计以下几种抽奖游戏：
(1)游戏A：设计一个游戏，使任意抽取一个信封时，能抽到纸币的概率为
；
(2)游戏B：设计一个游戏，使任意抽取一个信封时，能抽到纸币的概率为
.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】(1)在平面直角坐标系中，作出下列各点，A（－3，4）， B（－3，－2），O（0，0），并把各点连起来.
（2）画出△ABO先向下平移2个单位，再向右平移4 个单位得到的图形△A1B1o1，并直接写出A1坐标
(3) 直接写出三角形ABO的面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AB=AC=5，BC=6，AD是BC边上的中线且AD=4，
是AD上的动点，
是AC边上的动点，则
的最小值是（ ）.
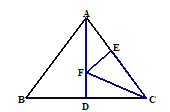
A. 6 B. 4 C. 
D. 不存在最小值
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，矩形OABC的顶点A、C坐标分别是（8，0），（0，4），反比例函数y= 
（x＞0）的图象过对角线的交点P并且与AB、BC分别交于D、E两点，连接OD、OE、DE，则△ODE的面积为（ ）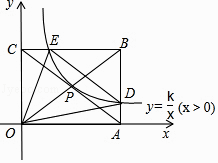 
A.14
B.12
C.15
D.8
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面的解题过程并回答问题.
解方程:
.
解:①当
时，原方程可化为
，解得
.经检验，符合题意；
②当
时，原方程可化为
，解得
.经检验，x的值不合题意，舍去;
③当
时，原方程可化为
，解得
音.经检验，符合题意.
所以原方程的解是或.
(1)根据上面的解题过程，求方程
的解;
(2)根据上面的解题过程，求方程
的解;
(3)方程
解.(填“有”或“无”)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，O为直线AB上一点，∠AOC＝50°，OD平分∠AOC，∠DOE＝90°.
(1)请你数一数，图中有多少个小于平角的角；
(2)求出∠BOD的度数；
(3)请通过计算说明OE是否平分∠BOC.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
