
����Ŀ��ij��������˾��������50�����г���������������Ϊÿ��ÿ��200Ԫʱ��ȫ������������ÿ���10Ԫ�����ȥ�ij��ͼ���2����
��1���������߶���Ԫʱ����˾��ÿ������ɴﵽ10120Ԫ��
��2����˾�쵼ϣ��������ﵽ10200Ԫ������Ϊ�ܷ�ʵ�֣����ܣ������ʱ����������ܣ���˵�����ɣ�
��3�������ճ�ά��Ҫһ�����ã���֪�����ÿ��ά����Ϊ100Ԫ��δ����ij���ά����Ϊ50Ԫ�������Ϊ����Ԫʱ����˾������ǡ��Ϊ5500Ԫ������������һά���ѣ���
���𰸡���1����������20Ԫ��30Ԫʱ����˾��ÿ������ɴﵽ10120Ԫ����2�������治�ܴﵽ10200Ԫ����3�������Ϊ250Ԫʱ����˾������ǡ��Ϊ5500Ԫ��
��������
��1����������xԪ����ÿ�տ������50![]() ���������������ÿ��������������������ɵó�����x��һԪ���η��̣���֮���ɵó����ۣ�
���������������ÿ��������������������ɵó�����x��һԪ���η��̣���֮���ɵó����ۣ�
��2�����������ÿ��������������������ɵó�����x��һԪ���η��̣��ɸ����б�ʽ����0�����ɵó���һԪ���η����⣬�����ɵó������治�ܴﵽ10200Ԫ��
��3�����������ÿ����������������������������ά���ѣ����ɵó�����x��һԪ���η��̣���֮���ɵó����ۣ�
��1����������xԪ����ÿ�տ������50��![]() ������
������
�������⣬�ã���200+x����50��![]() ����10120��
����10120��
�������ã�x2��50x+600��0��
��ã�x1��20��x2��30��
�𣺵�������20Ԫ��30Ԫʱ����˾��ÿ������ɴﵽ10120Ԫ��
��2��������ʵ�֣�
�����⣬�ã���200+x����50��![]() ����10200��
����10200��
�������ã�x2��50x+1000��0��
��![]() ������50��2��4��1��1000����1500��0��
������50��2��4��1��1000����1500��0��
����һԪ���η����⣬
�������治�ܴﵽ10200Ԫ��
��3�������⣬�ã���200+x����50��![]() ����100��50��
����100��50��![]() ����50��
����50��![]() ��5500��
��5500��
�������ã�x2��100x+2500��0��
��ã�x1��x2��50��
��200+x��250��
�𣺵����Ϊ250Ԫʱ����˾������ǡ��Ϊ5500Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
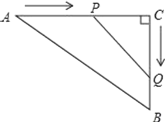
����Ŀ����ͼ���ڡ�ABC�У�AB��10![]() m��BC��40m����C��90�㣬��P�ӵ�A��ʼ�ر�AC�����C��2m/s���ٶ������ƶ���ͬʱ��һ��Q��C�㿪ʼ��3m/s���ٶ����ű�CB�����ƶ�������ʱ����PCQ���������432m2��
m��BC��40m����C��90�㣬��P�ӵ�A��ʼ�ر�AC�����C��2m/s���ٶ������ƶ���ͬʱ��һ��Q��C�㿪ʼ��3m/s���ٶ����ű�CB�����ƶ�������ʱ����PCQ���������432m2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10�֣�ˮ�����Ű�����ÿ��2Ԫ�ļ۸�ij��ˮ�����ɽȻ����ÿ��4Ԫ�ļ۸���ۣ�ÿ����۳�100�ͨ�����鷢�֣�����ˮ��ÿ����ۼ�ÿ����0.1Ԫ��ÿ��ɶ��۳�20�Ϊ��֤ÿ�������۳�260��Ű��̾����������ۣ�
��1����������ˮ��ÿ����ۼ۽���xԪ����ÿ����������� ��ú�x�Ĵ���ʽ��ʾ����
��2����������ˮ��Ҫ��ÿ��ӯ��300Ԫ���Ű����轫ÿ����ۼ۽��Ͷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
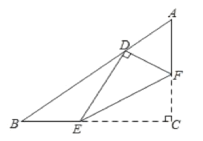
����Ŀ����ͼ,��Rt��ABC��,��C=90����AC=3��BC=4����E��F�ֱ��ڱ�BC��AC�ϣ���EF���ڵ�ֱ���۵���C��ʹ��C�Ķ�Ӧ��Dǡ�����ڱ�AB�ϣ�����EFC�͡�ABC���ƣ���AD�ij�Ϊ___.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
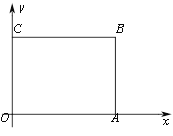
����Ŀ����ͼ����ֱ������ϵ�У�����OABC�ı�OA��x���ϣ�OC��y���ϣ���B������Ϊ��8��6��������D��B���������1����λ����ÿ����ٶ���C���˶�t�루D����B��C�غϣ�������AD������ABD��AD��������AB'D��B'�ھ��ε��ڲ�����ϣ�������DB'��DB'����ֱ����AC���ڵ�F����OA����ֱ�߽��ڵ�E��
��1���ٵ�t�� �룬B'��F�غϣ�
�����߶�CB'��ȡֵ��Χ��
��2������EB'�ij��ȣ��ú�t�Ĵ���ʽ��ʾ���������t��ȡֵ��Χ��
�ڵ�tΪ��ֵʱ����AEF����AEΪ�ĵ��������Σ��������ʱEC�ij��ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=��1����x���һ������A�ڵ㣨��3��0���ͣ���2��0��֮�䣬�䲿��ͼ����ͼ�������н��ۣ���4ac��b2��0����2a��b=0����a+b+c��0���ܵ�M��x1��y1����N��x2��y2�����������ϣ���x1��x2����1����y1��y2����abc��0��������ȷ���۵ĸ����ǣ�������
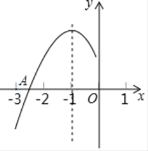
A.5��B.4��C.3��D.2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��װ������ij�ַ�װ��ÿ���ɱ�Ϊ65Ԫ���涨������10��������������������y��Ԫ/��������������x��������xΪ��������֮��������ĺ�����ϵ��ͼ��ʾ��
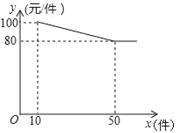
(1)��y��x֮��������ĺ�����ϵʽ����д��x��ȡֵ��Χ��
(2)��10��x��50��xΪ�������������������ַ�װ���ټ�ʱ����װ���������600Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ˮ�����Ű�����ÿ��2Ԫ�ļ۸�ij��ˮ�����ɽȻ����ÿ��4Ԫ�ļ۸���ۣ�ÿ����۳�100�ͨ�����鷢�֣�����ˮ��ÿ����ۼ�ÿ����0.1Ԫ��ÿ��ɶ��۳�20�Ϊ��֤ÿ�������۳�260��Ű��̾����������ۣ�
��������ˮ��Ҫ��ÿ��ӯ��300Ԫ���Ű����轫ÿ����ۼ۽��Ͷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=![]() x+2�ֱ�x��y���ڵ�A��C����P�Ǹ�ֱ���뷴��������y=
x+2�ֱ�x��y���ڵ�A��C����P�Ǹ�ֱ���뷴��������y=![]() ��ͼ���ڵ�һ�����ڵĽ��㣬PB�Ax�ᣬBΪ���㣬S��ABP=9��
��ͼ���ڵ�һ�����ڵĽ��㣬PB�Ax�ᣬBΪ���㣬S��ABP=9��
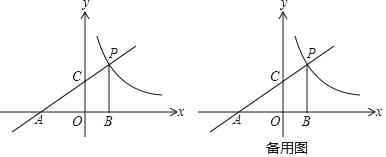
��1��ֱ��д����A������_____����C������_____����P������_____��
��2����֪��Q�ڷ���������y=![]() ��ͼ���ϣ��������Ϊ6����x����ȷ��һ��M��ʹMP+MQ��С��������ͼ�ۼ������������M�����ꣻ
��ͼ���ϣ��������Ϊ6����x����ȷ��һ��M��ʹMP+MQ��С��������ͼ�ۼ������������M�����ꣻ
��3�����R�ڷ���������y=![]() ��ͼ���ϣ�����ֱ��PB���Ҳ࣬��RT��x�ᣬTΪ���㣬����BRT���AOC����ʱ�����R�����꣮
��ͼ���ϣ�����ֱ��PB���Ҳ࣬��RT��x�ᣬTΪ���㣬����BRT���AOC����ʱ�����R�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com