
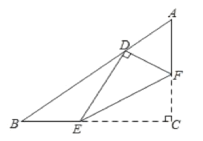
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E,F分别在边BC,AC上,沿EF所在的直线折叠∠C,使点C的对应点D恰好落在边AB上,若△EFC和△ABC相似,则AD的长为___.
【答案】![]()
【解析】
△CEF与△ABC相似,分两种情况:①若CF:CE=3:4,此时EF∥AB,CD为AB边上的高;②若CE:CF=3:4,由相似三角形角之间的关系,可以推出∠B=∠ECD与∠A=∠FCD,从而得到CD=AD=BD,即D点为AB的中点.
若△CEF与△ABC相似,分两种情况:
①若CF:CE=3:4,
∵AC:BC=3:4,
∴CF:CE=AC:BC,
∴EF∥AB.
连接CD,如图1所示:
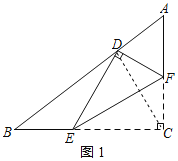
由折叠性质可知,CD⊥EF,
∴CD⊥AB,即此时CD为AB边上的高。
在Rt△ABC中,∵∠ACB=90°,AC=3,BC=4,
∴AB=![]() =5,
=5,
∴cosA=![]() ,
,
∴AD=ACcosA=3×![]() ;
;
②若CE:CF=3:4,
∵AC:BC=3:4,∠C=∠C,
∵△CEF∽△CAB,
∴∠CEF=∠A.
连接CD,如图2所示:
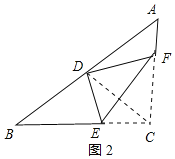
由折叠性质可知,∠CEF+∠ECD=90°,
又∵∠A+∠B=90°,
∴∠B=∠ECD,
∴BD=CD.
同理可得:∠A=∠FCD,AD=CD,
∴D点为AB的中点,
∴AD=![]() ;
;
故答案为:![]()


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】已知x1,x2是关于x的一元二次方程x2+2(m-3) x+m2+1=0的两个根.
(1)当m取何值时,方程有两个不相等的实数根?
(2)若以x1,x2为对角线的菱形边长是![]() ,试求m的值.
,试求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线![]() 和直线l:y=kx+b,点A(-3,-3),B(1,-1)均在直线l上.
和直线l:y=kx+b,点A(-3,-3),B(1,-1)均在直线l上.
(1)若抛物线C与直线l有交点,求a的取值范围;
(2)当a=-1,二次函数![]() 的自变量x满足m≤x≤m+2时,函数y的最大值为-4,求m的值;
的自变量x满足m≤x≤m+2时,函数y的最大值为-4,求m的值;
(3)若抛物线C与线段AB有两个不同的交点,请直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则
①二次函数的最大值为a+b+c;
②a﹣b+c<0;
③b2﹣4ac<0;
④当y>0时,﹣1<x<3,其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求解体验:
(1)已知抛物线 y=﹣x2+bx﹣3 经过点(﹣1,0),则 b= ,顶点坐标为 ,该抛物线关于点(0,1)成中心对称的抛物线表达式是 .
抽象感悟:
我们定义:对于抛物线 y=ax2+bx+c(a≠0),以 y 轴上的点 M(0,m)为中心,作该抛物线关于点 M 对称的 抛物线 y′,则我们又称抛物线 y′为抛物线 y 的“衍生抛物线”,点 M 为“衍生中心”.
(2)已知抛物线 y=﹣x2﹣2x+5 关于点(0,m)的衍生抛物线为 y′,若这两条抛物线有交点,求 m 的取值范 围.
问题解决:
(3)已知抛物线 y=ax2+2ax﹣b(a≠0)
①若抛物线 y 的衍生抛物线为 y′=bx2﹣2bx+a2(b≠0),两抛物线有两个交点,且恰好是它们的顶点,求 a、b 的值及衍生中心的坐标;
②若抛物线 y 关于点(0,k+12)的衍生抛物线为 y1,其顶点为 A1;关于点(0,k+22)的衍生抛物线为 y2,其顶点为 A2;…;关于点(0,k+n2)的衍生抛物线为 yn,其顶点为 An…(n 为正整数).求 An An+1 的长(用含 n 的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】. 在一个不透明的布袋中装有三个小球,小球上分别标有数字﹣1、0、2,它们除了数字不同外,其他都完全相同.
(1)随机地从布袋中摸出一个小球,则摸出的球为标有数字2的小球的概率为 ;
(2)小丽先从布袋中随机摸出一个小球,记下数字作为平面直角坐标系内点M的横坐标.再将此球放回、搅匀,然后由小华再从布袋中随机摸出一个小球,记下数字作为平面直角坐标系内点M的纵坐标,请用树状图或表格列出点M所有可能的坐标,并求出点M落在如图所示的正方形网格内(包括边界)的概率.
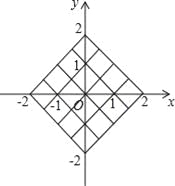
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转45°得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1OD的面积是(____)
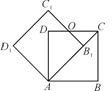
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中正确的是( )
A. 抛物线与x轴的一个交点为(4,0)
B. 函数y=ax2+bx+c的最大值为6
C. 抛物线的对称轴是x=![]()
D. 在对称轴右侧,y随x增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
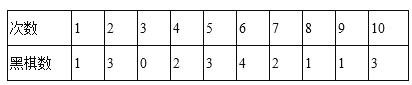
根据以上数据,估算袋中的白棋子数量为( )
A. 60枚B. 50枚C. 40枚D. 30枚
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com