
【题目】求解体验:
(1)已知抛物线 y=﹣x2+bx﹣3 经过点(﹣1,0),则 b= ,顶点坐标为 ,该抛物线关于点(0,1)成中心对称的抛物线表达式是 .
抽象感悟:
我们定义:对于抛物线 y=ax2+bx+c(a≠0),以 y 轴上的点 M(0,m)为中心,作该抛物线关于点 M 对称的 抛物线 y′,则我们又称抛物线 y′为抛物线 y 的“衍生抛物线”,点 M 为“衍生中心”.
(2)已知抛物线 y=﹣x2﹣2x+5 关于点(0,m)的衍生抛物线为 y′,若这两条抛物线有交点,求 m 的取值范 围.
问题解决:
(3)已知抛物线 y=ax2+2ax﹣b(a≠0)
①若抛物线 y 的衍生抛物线为 y′=bx2﹣2bx+a2(b≠0),两抛物线有两个交点,且恰好是它们的顶点,求 a、b 的值及衍生中心的坐标;
②若抛物线 y 关于点(0,k+12)的衍生抛物线为 y1,其顶点为 A1;关于点(0,k+22)的衍生抛物线为 y2,其顶点为 A2;…;关于点(0,k+n2)的衍生抛物线为 yn,其顶点为 An…(n 为正整数).求 An An+1 的长(用含 n 的式子表示).
【答案】(1)b=-4,(-2,1),![]() ;(2)m≤5;(3)4n+2
;(2)m≤5;(3)4n+2
【解析】
求解体验:(1)利用待定系数法求出b的值,进而求出顶点坐标,在抛物线上取一点(0,-3),求出点(-2,1)和(0,-3)关于(0,1)的对称点坐标,利用待定系数法即可得出结论;
抽象感悟:(2)求出抛物线的顶点坐标(-1,6),进而利用待定系数法求出衍生函数解析式,联立即可得出结论;
问题解决:(3)①求出抛物线的顶点坐标和衍生抛物线的顶点坐标,分别代入抛物线解析式中,即可求出a,b的值,即可得出结论;
②求出抛物线顶点关于(0,k+n2)和(0,k+(n+1)2)的对称点坐标,即可得出结论.
解:求解体验:(1)∵抛物线y=-x2+bx-3经过点(-1,0),
∴-1-b-3=0,
∴b=-4,
∴抛物线解析式为y=-x2-4x-3=-(x+2)2+1,
∴抛物线的顶点坐标为(-2,1),
∴抛物线的顶点坐标(-2,1)关于(0,1)的对称点为(2,1),
即:新抛物线的顶点坐标为(2,1),
令原抛物线的x=0,
∴y=-3,
∴(0,-3)关于点(0,1)的对称点坐标为(0,5),
设新抛物线的解析式为y=a(x-2)2+1,
∵点(0,5)在新抛物线上,
∴5=a(0-2)2+1,
∴a=1,
∴新抛物线解析式为y=(x-2)2+1=x2-4x+5,
故答案为-4,(-2,1),y=x2-4x+5;
抽象感悟:(2)∵抛物线y=-x2-2x+5=-(x+1)2+6①,
∴抛物线的顶点坐标为(-1,6),
设衍生抛物线为y′=a(x-1)2+2m-6,
∵抛物线y=-x2-2x+5关于点(0,m)的衍生抛物线为y′,
∴a=1,
∴衍生抛物线为y′=(x-1)2+2m-6=x2-2x+2m-5②,
联立①②得,x2-2x+2m-5=-x2-2x+5,
整理得,2x2=10-2m,
∵这两条抛物线有交点,
∴10-2m≥0,
∴m≤5;
问题解决:
(3)①抛物线y=ax2+2ax-b=a(x+1)2-a-b,
∴此抛物线的顶点坐标为(-1,-a-b),
∵抛物线y的衍生抛物线为y′=bx2-2bx+a2=b(x-1)2+a2-b,
∴a+b=0,③
∵两个抛物线有两个交点,且恰好是它们的顶点,
∴b+2b+a2=-a-b④,
联立③④,∴a=0(舍)或a=3,
∴b=-3,
∴抛物线y的顶点坐标为(-1,0),抛物线y的衍生抛物线的顶点坐标为(1,12),
∴衍生中心的坐标为(0,6);
②抛物线y=ax2+2ax-b的顶点坐标为(-1,-a-b),
∵点(-1,-a-b)关于点(0,k+n2)的对称点为(1,a+b+2k+2n2),
∴抛物线yn的顶点坐标An为(1,a+b+2k+2n2),
同理:An+1(1,a+b+2k+2(n+1)2)
∴AnAn+1=a+b+2k+2(n+1)2-(a+b+2k+2n2)=4n+2.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克![]() 元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克
元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克![]() 元,经试销发现,销售量
元,经试销发现,销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)符合一次函数关系,如图是
(元)符合一次函数关系,如图是![]() 与
与![]() 的函数关系图象.
的函数关系图象.
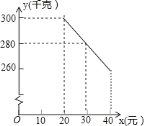
![]() 求
求![]() 与
与![]() 的函数解析式(也称关系式);
的函数解析式(也称关系式);
![]() 设该水果销售店试销草莓获得的利润为
设该水果销售店试销草莓获得的利润为![]() 元,求
元,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数![]() 和一次函数
和一次函数![]() ,我们把
,我们把 ![]() 称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E.现有点A(1,0)和抛物线E上的点B(2,n),请完成下列任务:
称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线E.现有点A(1,0)和抛物线E上的点B(2,n),请完成下列任务:
(尝试)
(1)当t=2时,抛物线![]() 的顶点坐标为 .
的顶点坐标为 .
(2)判断点A是否在抛物线E上;
(3)求n的值.
(发现)通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线E总过定点,定点的坐标 .
(应用)二次函数![]() 是二次函数
是二次函数![]() 和一次函数
和一次函数 ![]() 的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x![]() +bx+c,经过点A(0,5)和点B(3,2)
+bx+c,经过点A(0,5)和点B(3,2)
(1)求抛物线的解析式:
(2)现有一半径为l,圆心P在抛物线上运动的动圆,问⊙P在运动过程中,是否存在⊙P与坐标轴相切的情况?若存在,请求出圆心P的坐标:若不存在,请说明理由;
(3)若⊙Q的半径为r,点Q 在抛物线上、⊙Q与两坐轴都相切时求半径r的值
查看答案和解析>>
科目:初中数学 来源: 题型:
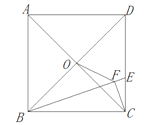
【题目】如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点.点E在CD上,且DE=2CE,连接BE.过点C作CF⊥BE,垂足是F,连接OF,则OF的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
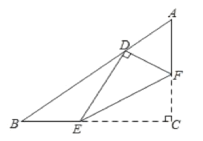
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点E,F分别在边BC,AC上,沿EF所在的直线折叠∠C,使点C的对应点D恰好落在边AB上,若△EFC和△ABC相似,则AD的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
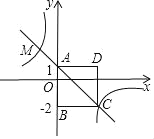
【题目】如图,四边形ABCD为正方形,点A坐标为(0,1),点B坐标为(0,﹣2),反比例函数y=![]() 的图象经过点C,一次函数y=ax+b的图象经过A、C两点.
的图象经过点C,一次函数y=ax+b的图象经过A、C两点.
(1)求反比例函数与一次函数的解析式;
(2)若点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,两人![]() 次测试成绩(单位:分)如下:
次测试成绩(单位:分)如下:
甲:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 乙:
乙:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
回答下列问题:
(1)甲成绩的平均数是 ,乙成绩的平均数是 ;
(2)如果从甲、乙两人![]() 次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于
次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于![]() 分的概率.(用列表或画树状图的方法)
分的概率.(用列表或画树状图的方法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形OABC的顶点坐标分别是O(0,0),A(3,0),B(4,4),C(-2,3),将点O,A,B,C的横坐标、纵坐标都乘以-2.
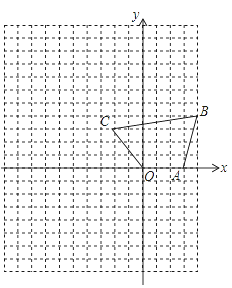
(1)画出以变化后的四个点为顶点的四边形;
(2)由(1)得到的四边形与四边形OABC位似吗?如果位似,指出位似中心及与原图形的相似比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com