
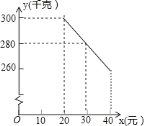
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克![]() 元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克
元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克![]() 元,经试销发现,销售量
元,经试销发现,销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)符合一次函数关系,如图是
(元)符合一次函数关系,如图是![]() 与
与![]() 的函数关系图象.
的函数关系图象.
![]() 求
求![]() 与
与![]() 的函数解析式(也称关系式);
的函数解析式(也称关系式);
![]() 设该水果销售店试销草莓获得的利润为
设该水果销售店试销草莓获得的利润为![]() 元,求
元,求![]() 的最大值.
的最大值.
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
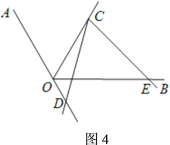
【题目】如图,已知![]() 与
与![]() ,
,![]() 平分
平分![]() .
.
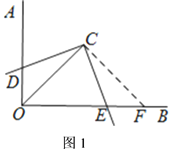
(1)如图1,![]() 与
与![]() 的两边分别相交于点
的两边分别相交于点![]() 、
、![]() ,
,![]() ,试判断线段
,试判断线段![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
以下是小宇同学给出如下正确的解法:
解:![]() .
.
理由如下:如图1,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() ,
,
…
请根据小宇同学的证明思路,写出该证明的剩余部分.
(2)你有与小宇不同的思考方法吗?请写出你的证明过程.
(3)若![]() ,
,![]() .
.
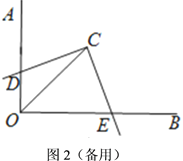
①如图3,![]() 与
与![]() 的两边分别相交于点
的两边分别相交于点![]() 、
、![]() 时,(1)中的结论成立吗?为什么?线段
时,(1)中的结论成立吗?为什么?线段![]() 、
、![]() 、
、![]() 有什么数量关系?说明理由.
有什么数量关系?说明理由.
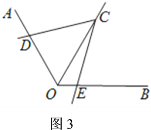
②如图4,![]() 的一边与
的一边与![]() 的延长线相交时,请回答(1)中的结论是否成立,并请直接写出线段
的延长线相交时,请回答(1)中的结论是否成立,并请直接写出线段![]() 、
、![]() 、
、![]() 有什么数量关系;如图5,
有什么数量关系;如图5,![]() 的一边与
的一边与![]() 的延长线相交时,请回答(1)中的结论是否成立,并请直接写出线段
的延长线相交时,请回答(1)中的结论是否成立,并请直接写出线段![]() 、
、![]() 、
、![]() 有什么数量关系.
有什么数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王教授和他的孙子小强星期天一起去爬山,来到山脚下,小强让爷爷先上山,然后追赶爷爷,如图所示,两条线段分别表示小强和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(小强开始爬山时开始计时),请看图回答下列问题:
(1)爷爷比小强先上了多少米?山顶离山脚多少米?
(2)谁先爬上山顶?小强爬上山顶用了多少分钟?
(3)图中两条线段的交点表示什么意思?这时小强爬山用时多少?离山脚多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
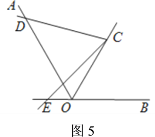
【题目】如图1,在四边形ABCD的边BC的延长线上取一点E,在直线BC的同侧作一个以CE为底的等腰△CEF,且满足∠B+∠F=180°,则称三角形CEF为四边形ABCD的“伴随三角形”.
(1)如图1,若△CEF是正方形ABCD的“伴随三角形”:
①连接AC,则∠ACF= ;
②若CE=2BC,连接AE交CF于H,求证:H是CF的中点;
(2)如图2,若△CEF是菱形ABCD的“伴随三角形”,∠B=60°,M是线段AE的中点,连接DM、FM,猜想并证明DM与FM的位置与数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
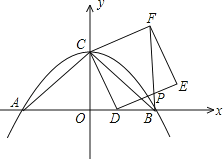
【题目】如图,抛物线y=﹣![]() x2+4交x轴于点A、B,交y轴于点C,连结AC,BC,D是线段OB上一动点,以CD为一边向右侧作正方形CDEF,连结BF,交DE于点P.
x2+4交x轴于点A、B,交y轴于点C,连结AC,BC,D是线段OB上一动点,以CD为一边向右侧作正方形CDEF,连结BF,交DE于点P.
(1)试判断△ABC的形状,并说明理由;
(2)求证:BF⊥AB.
(3)当点D从点O沿x轴正方向移动到点B时,点E所走过的路线长为______;
(4)探究当点D在何处时,△FBC是等腰三角形,并求出相应的BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知:![]() ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么![]() ABCD的周长是多少?
ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成正方形零件如图1,使正方形的一边在BC上,其余两个顶点分别在AB、AC上.

(1)求证:△AEF∽△ABC;
(2)求这个正方形零件的边长;
(3)如果把它加工成矩形零件如图2,问这个矩形的最大面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com