
【题目】已知点A(t,y1),B(t+2,y2)在抛物线y=﹣![]() x2的图象上,且﹣2≤t≤2,则线段AB长的最大值______.
x2的图象上,且﹣2≤t≤2,则线段AB长的最大值______.
【答案】2![]()
【解析】
由点A、B在抛物线上,可用t表示y1、y2,根据两点间距离公式用t表示AB2,发现AB2与t是二次函数的关系,由抛物线性质和自变量t的取值范围可知:t在对称轴上时取得最小值;观察t本身的取值范围,看t=﹣2和t=2哪个离对称轴更远,即对应的函数值最大.
解:∵点A(t,y1),B(t+2,y2)在抛物线y=﹣![]() x2的图象上,
x2的图象上,
∴y1=﹣![]() t2,y2=﹣
t2,y2=﹣![]() (t+2)2=﹣
(t+2)2=﹣![]() t2﹣2t﹣2,
t2﹣2t﹣2,
∴AB2=(t+2﹣t)2+(y2﹣y1)2
=22+(﹣![]() t2﹣2t﹣2+
t2﹣2t﹣2+![]() t2)2
t2)2
=4+(﹣2t﹣2)2
=4(t+1)2+4
∴AB2与t是二次函数的关系,由抛物线性质可知:
当t=﹣1时,AB2取得最小值,AB2=4,AB=2
当t=2时,AB2取得最大值,AB2=4×(2+1)2+4=40,AB=2![]() ,
,
故答案为:2![]() .
.


科目:初中数学 来源: 题型:
【题目】(1)如图1,已知![]() 中,
中,![]() ,
,![]() ,垂足为
,垂足为![]() ,
,![]() ,则
,则![]() ___
___![]() .
.
(2)若把(1)中![]() 改为
改为![]() ,其它条件不变,请用含
,其它条件不变,请用含![]() 的式子表示
的式子表示![]() ,并证明 你的结论.
,并证明 你的结论.
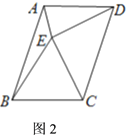
(3)如图2,四边形![]() 中,
中,![]() ,点
,点![]() 在四边形
在四边形![]() 内部,在
内部,在![]() 中,
中,![]() ,且
,且![]() ,连接
,连接![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
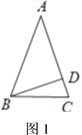
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发商以20元/千克的价格购入了某种水果100千克.据市场预测,该种水果的售价y(元/千克)与保存时间x(天)的函数关系为y=30+2x,但保存这批水果平均每天将损耗10千克,且最多能保存8天.另外,批发商保存该批水果每天还需20元的费用.
(1)若批发商保存1天后将该批水果一次性卖出,则卖出时水果的售价为 (元/千克),获得的总利润为 (元);
(2)设批发商在保存了x天后一次性卖出了保存水果,获得了200元的利润,求这批水果的保存时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数![]() .
.
![]() 它的图象与二次函数
它的图象与二次函数![]() 的图象有什么关系?它是轴对称图形吗?它的开口方向,对称轴和顶点坐标分别是什么?
的图象有什么关系?它是轴对称图形吗?它的开口方向,对称轴和顶点坐标分别是什么?
![]() 当
当![]() 取哪些值时,
取哪些值时,![]() 的值随
的值随![]() 的增大而增大?当
的增大而增大?当![]() 取哪些值时,
取哪些值时,![]() 的值随
的值随![]() 的增大而减小?
的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克![]() 元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克
元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克![]() 元,经试销发现,销售量
元,经试销发现,销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)符合一次函数关系,如图是
(元)符合一次函数关系,如图是![]() 与
与![]() 的函数关系图象.
的函数关系图象.
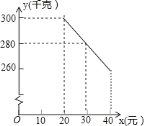
![]() 求
求![]() 与
与![]() 的函数解析式(也称关系式);
的函数解析式(也称关系式);
![]() 设该水果销售店试销草莓获得的利润为
设该水果销售店试销草莓获得的利润为![]() 元,求
元,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某农场老板准备建造一个矩形羊圈![]() ,他打算让矩形羊圈的一面完全靠着墙
,他打算让矩形羊圈的一面完全靠着墙![]() ,墙
,墙![]() 可利用的长度为
可利用的长度为![]() ,另外三面用长度为
,另外三面用长度为![]() 的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分)
的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分)

![]() 若要使矩形羊圈的面积为
若要使矩形羊圈的面积为![]() ,则垂直于墙的一边长
,则垂直于墙的一边长![]() 为多少米?
为多少米?
![]() 农场老板又想将羊圈
农场老板又想将羊圈![]() 的面积重新建造成面积为
的面积重新建造成面积为![]() ,从而可以养更多的羊,请聪明的你告诉他:他的这个想法能实现吗?为什么?
,从而可以养更多的羊,请聪明的你告诉他:他的这个想法能实现吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出 4台.商场要想在这种冰箱销售中每天盈利 4800 元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
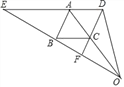
【题目】如图,已知DE∥BC,AO,DF交于点C.∠EAB=∠BCF.
(1)求证:AB∥DF;
(2)求证:OB2=OEOF;
(3)连接OD,若∠OBC=∠ODC,求证:四边形ABCD为菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com