
【题目】(1)如图1,已知![]() 中,
中,![]() ,
,![]() ,垂足为
,垂足为![]() ,
,![]() ,则
,则![]() ___
___![]() .
.
(2)若把(1)中![]() 改为
改为![]() ,其它条件不变,请用含
,其它条件不变,请用含![]() 的式子表示
的式子表示![]() ,并证明 你的结论.
,并证明 你的结论.
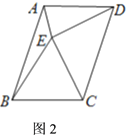
(3)如图2,四边形![]() 中,
中,![]() ,点
,点![]() 在四边形
在四边形![]() 内部,在
内部,在![]() 中,
中,![]() ,且
,且![]() ,连接
,连接![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
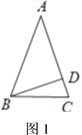
【答案】(1)20°;(2)![]() ;(3)∠AEB=135°.
;(3)∠AEB=135°.
【解析】
(1)在△ABC中利用等腰三角形性质与三角形内角和得到∠C=70°,再利用直角三角形性质在直角三角形BCD中,即可得到∠DBC;(2)在△ABC中利用等腰三角形性质与三角形内角和得到![]() ,再利用直角三角形性质在直角三角形BCD中,即可得到
,再利用直角三角形性质在直角三角形BCD中,即可得到![]() ;(3)过点
;(3)过点![]() 作
作![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,在△DEC、△ADE、△BCE中利用三角形内角和定理,列出关系式,利用等量代换关系即可求解.
,在△DEC、△ADE、△BCE中利用三角形内角和定理,列出关系式,利用等量代换关系即可求解.
(1)∵ ![]() ,
,![]()
∴∠C=![]() =70°
=70°
又∵![]()
∴∠BDC=90°
∴∠DBC=90°-70°=20°
(2)![]()
证明:![]() ,
,
![]() ,
,
![]()
![]() 在
在![]() 中,
中,
![]() .
.
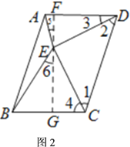
(3)过点![]() 作
作![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,
,
则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
由(2)得![]() ,
,
![]() ,
,
![]() .
.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
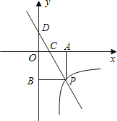
【题目】如图,一次函数![]() 的图象分别交
的图象分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、点
、点![]() ,与反比例函数
,与反比例函数![]() 的图象在第四象限的相交于点
的图象在第四象限的相交于点![]() ,并且
,并且![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,已知
,已知![]() ,且
,且![]()
![]() 求上述一次函数与反比例函数的表达式;
求上述一次函数与反比例函数的表达式;
![]() 求一次函数与反比例函数的另一个交点坐标.
求一次函数与反比例函数的另一个交点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=2,AC=3,1<BC<5,分别以AB、BC、AC为边向外作正方形ABIH、BCDE和正方形ACFG,则图中阴影部分的最大面积为( )
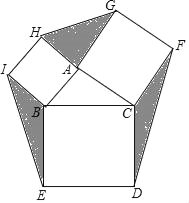
A. 6 B. 9 C. 11 D. 无法计算
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合).DE∥AB交AC于点F,CE∥AM,连结AE.
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长BD交AC于点H,若BH⊥AC,且BH=AM.
①求∠CAM的度数;
②当FH=![]() ,DM=4时,求DH的长.
,DM=4时,求DH的长.
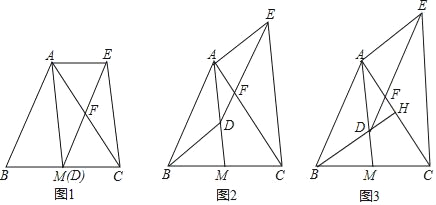
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 与
与![]() ,
,![]() 平分
平分![]() .
.
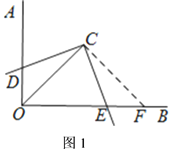
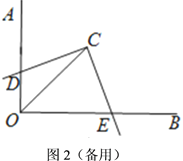
(1)如图1,![]() 与
与![]() 的两边分别相交于点
的两边分别相交于点![]() 、
、![]() ,
,![]() ,试判断线段
,试判断线段![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
以下是小宇同学给出如下正确的解法:
解:![]() .
.
理由如下:如图1,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() ,
,
…
请根据小宇同学的证明思路,写出该证明的剩余部分.
(2)你有与小宇不同的思考方法吗?请写出你的证明过程.
(3)若![]() ,
,![]() .
.
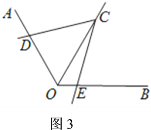
①如图3,![]() 与
与![]() 的两边分别相交于点
的两边分别相交于点![]() 、
、![]() 时,(1)中的结论成立吗?为什么?线段
时,(1)中的结论成立吗?为什么?线段![]() 、
、![]() 、
、![]() 有什么数量关系?说明理由.
有什么数量关系?说明理由.
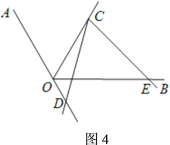
②如图4,![]() 的一边与
的一边与![]() 的延长线相交时,请回答(1)中的结论是否成立,并请直接写出线段
的延长线相交时,请回答(1)中的结论是否成立,并请直接写出线段![]() 、
、![]() 、
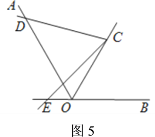
、![]() 有什么数量关系;如图5,
有什么数量关系;如图5,![]() 的一边与
的一边与![]() 的延长线相交时,请回答(1)中的结论是否成立,并请直接写出线段
的延长线相交时,请回答(1)中的结论是否成立,并请直接写出线段![]() 、
、![]() 、
、![]() 有什么数量关系.
有什么数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中△ABC三个顶点的坐标分别是点A(﹣2,3)、点B(﹣1,1)、点C(0,2).
(1)作△ABC关于C成中心对称的△A1B1C1;
(2)将△A1B1C1向右平移3个单位,作出平移后的△A2B2C2;
(3)在x轴上求作一点P,使PA1+PC1的值最小,并写出点 P 的坐标.(不写解答过程,直接写出结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市某一城市美化工程招标时,有甲、乙两个工程队投标,经测算:甲队单独完成这项工程需要60天,若由甲队先做20天,剩下的工程由甲、乙合作24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com