
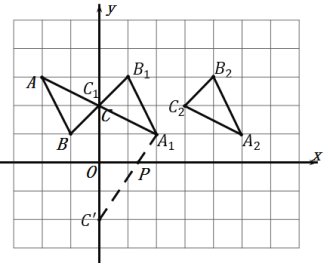
【题目】如图所示,在平面直角坐标系中△ABC三个顶点的坐标分别是点A(﹣2,3)、点B(﹣1,1)、点C(0,2).
(1)作△ABC关于C成中心对称的△A1B1C1;
(2)将△A1B1C1向右平移3个单位,作出平移后的△A2B2C2;
(3)在x轴上求作一点P,使PA1+PC1的值最小,并写出点 P 的坐标.(不写解答过程,直接写出结果)

【答案】(1)见解析;(2)见解析;(3)(![]() ,0)
,0)
【解析】
(1)根据关于原点对称的点的坐标特征分别作出点A、B、C关于原点的对称点A1、B1、C1,即可得到△A1B1C1;
(2)根据平移的性质分别作出点A1、B1、C1对称点A2、B2、C2,即可得到△A2B2C2;
(3)由于点C′和C1关于x轴对称,连结C′A1交x轴于P,则PC′=PC1,所以PC1+PA1=PC′+PA1=C′A1,根据两点之间线段最短得到PA1+PC1的值最小,接着利用待定系数法求出直线C′A1的解析式为y=![]() x﹣2,然后计算函数为0时的自变量的值即可得到点P的坐标.
x﹣2,然后计算函数为0时的自变量的值即可得到点P的坐标.
(1)如图,△A1B1C1为所求;
(2)如图,△A2B2C2为所求;
(3)作点C1关于x轴对称的对称点C′,连结C′A1交x轴于P,则PC′=PC1,
则PC1+PA1=PC′+PA1=C′A1,
此时PA1+PC1的值最小,
设直线C′A1的解析式为y=kx+b,
∵点C1的坐标为:![]() ,
,
∴点C′的坐标为:![]() ,
,
把C′(0,﹣2),A1(2,1)代入得![]() ,解得
,解得 ,
,
所以直线C′A1的解析式为![]() ,
,
当y=0时![]() ,解得
,解得![]() ,
,
所以点P的坐标为(![]() ,0).
,0).


科目:初中数学 来源: 题型:
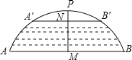
【题目】如图所示,有一座拱桥圆弧形,它的跨度![]() 为
为![]() 米,拱高为
米,拱高为![]() 米,当洪水泛滥到跨度只有
米,当洪水泛滥到跨度只有![]() 米时,就要采取紧急措施,若拱顶离水面只有
米时,就要采取紧急措施,若拱顶离水面只有![]() 米,即
米,即![]() 米时,试通过计算说明是否需要采取紧急措施?
米时,试通过计算说明是否需要采取紧急措施?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知![]() 中,
中,![]() ,
,![]() ,垂足为
,垂足为![]() ,
,![]() ,则
,则![]() ___
___![]() .
.
(2)若把(1)中![]() 改为
改为![]() ,其它条件不变,请用含
,其它条件不变,请用含![]() 的式子表示
的式子表示![]() ,并证明 你的结论.
,并证明 你的结论.
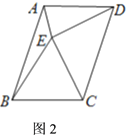
(3)如图2,四边形![]() 中,
中,![]() ,点
,点![]() 在四边形
在四边形![]() 内部,在
内部,在![]() 中,
中,![]() ,且
,且![]() ,连接
,连接![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
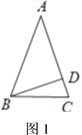
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两位同学用围棋子做游戏.如图所示,现轮到黑棋下子,黑棋下一子后白棋再下一子,使黑棋的5个棋子组成轴对称图形,白棋的5个棋子也成轴对称图形.则下列下子方法不正确的是【 】.[说明:棋子的位置用数对表示,如A点在(6,3)]

A.黑(3,7);白(5,3) B.黑(4,7);白(6,2)
C.黑(2,7);白(5,3) D.黑(3,7);白(2,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一段![]() 米长的河堤的整治任务,打算请
米长的河堤的整治任务,打算请![]() 两个工程队来完成,经过调查发现,
两个工程队来完成,经过调查发现,![]() 工程队每天比
工程队每天比![]() 工程队每天多整治
工程队每天多整治![]() 米,
米,![]() 工程队单独整治的工期是
工程队单独整治的工期是![]() 工程队单独整治的工期的
工程队单独整治的工期的![]() .
.
(1)问![]() 工程队每天分别整治多少米?
工程队每天分别整治多少米?
(2)由![]() 两个工程队先后接力完成,共用时
两个工程队先后接力完成,共用时![]() 天,问
天,问![]() 工程队分别整治多少米?
工程队分别整治多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发商以20元/千克的价格购入了某种水果100千克.据市场预测,该种水果的售价y(元/千克)与保存时间x(天)的函数关系为y=30+2x,但保存这批水果平均每天将损耗10千克,且最多能保存8天.另外,批发商保存该批水果每天还需20元的费用.
(1)若批发商保存1天后将该批水果一次性卖出,则卖出时水果的售价为 (元/千克),获得的总利润为 (元);
(2)设批发商在保存了x天后一次性卖出了保存水果,获得了200元的利润,求这批水果的保存时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某农场老板准备建造一个矩形羊圈![]() ,他打算让矩形羊圈的一面完全靠着墙
,他打算让矩形羊圈的一面完全靠着墙![]() ,墙
,墙![]() 可利用的长度为
可利用的长度为![]() ,另外三面用长度为
,另外三面用长度为![]() 的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分)
的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分)

![]() 若要使矩形羊圈的面积为
若要使矩形羊圈的面积为![]() ,则垂直于墙的一边长
,则垂直于墙的一边长![]() 为多少米?
为多少米?
![]() 农场老板又想将羊圈
农场老板又想将羊圈![]() 的面积重新建造成面积为
的面积重新建造成面积为![]() ,从而可以养更多的羊,请聪明的你告诉他:他的这个想法能实现吗?为什么?
,从而可以养更多的羊,请聪明的你告诉他:他的这个想法能实现吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com