
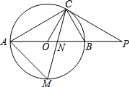
【题目】如图,已知点![]() 在
在![]() 上,延长直径
上,延长直径![]() 到点
到点![]() ,连接
,连接![]() ,
,![]() .
.
![]() 求证:
求证:![]() 是
是![]() 的切线;
的切线;
![]() 若
若![]() ,且
,且![]() ,
,![]() 是
是![]() 下半圆弧的中点,求
下半圆弧的中点,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)由于OA=OC,那么∠OAC=∠OCA,则∠COB=2∠OCA,又∠COB=2∠PCB,可求∠OCA=∠PCB,而AB是直径,可知∠OCA+∠OCB=90°,从而有∠PCB+∠OCB=90°,即∠OCP=90°,从而可证CP是⊙O切线;
(2)连接BM,由于M是弧AB中点,那么AM=BM,而∠AMB=90°,易知∠MAB=∠MBA=45°,而AC=CP,则∠P=∠CAO,又∠BCP=∠CAO,从而有∠P=∠BCP,即BC=BP=3,而∠CBO=2∠P,∠BOC=2∠CAO,于是∠BOC=∠CBO,而OB=OC,那么可证△BOC是等边三角形,从而有OB=BC=3,即AB=6,在Rt△AMB中,利用特殊三角函数值可求AM.
![]() ∵
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 直径,
直径,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵点![]() 在
在![]() 上,
上,
∴![]() 是
是![]() 的切线;
的切线;

![]() 连接
连接![]() .
.
∵![]() 是
是![]() 下半圆弧中点,
下半圆弧中点,
∴弧![]() 弧
弧![]() ,
,
∴![]() ,
,
∵![]() 是
是![]() 直径,
直径,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
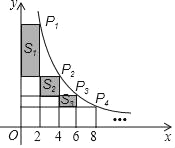
【题目】如图,在反比例函数y=![]() (x>0)的图象上,有点P1,P2,P3,P4,…,它们的横坐标依次为2,4,6,8,…分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次记为S1,S2,S3,…,Sn,则S1+S2+S3+…+Sn=_____(用含n的代数式表示)
(x>0)的图象上,有点P1,P2,P3,P4,…,它们的横坐标依次为2,4,6,8,…分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次记为S1,S2,S3,…,Sn,则S1+S2+S3+…+Sn=_____(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中△ABC三个顶点的坐标分别是点A(﹣2,3)、点B(﹣1,1)、点C(0,2).
(1)作△ABC关于C成中心对称的△A1B1C1;
(2)将△A1B1C1向右平移3个单位,作出平移后的△A2B2C2;
(3)在x轴上求作一点P,使PA1+PC1的值最小,并写出点 P 的坐标.(不写解答过程,直接写出结果)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识背景:我们在第十一章《三角形》中学习了三角形的边与角的性质,在第十二章《全等三角形》中学习了全等三角形的性质和判定,在第十三章《轴对称》中学习了等腰三角形的性质和判定.在一些探究题中经常用以上知识转化角和边,进而解决问题.
问题:如图1,![]() 是等腰三角形,
是等腰三角形,![]() ,
,![]() 是
是![]() 的中点,以
的中点,以![]() 为腰作等腰
为腰作等腰![]() ,且满足
,且满足![]() ,连接
,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() ,试探究
,试探究![]() 与
与![]() 之间的数量关系.
之间的数量关系.
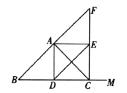
图1
发现:(1)![]() 与
与![]() 之间的数量关系为 .
之间的数量关系为 .
探究:(2)如图2,当点![]() 是线段
是线段![]() 上任意一点(除
上任意一点(除![]() 、
、![]() 外)时,其他条件不变,试猜想
外)时,其他条件不变,试猜想![]() 与
与![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
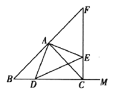
图2
拓展:(3)当点![]() 在线段
在线段![]() 的延长线上时,在备用图中补全图形,并直接写出
的延长线上时,在备用图中补全图形,并直接写出![]() 的形状.
的形状.

备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市某一城市美化工程招标时,有甲、乙两个工程队投标,经测算:甲队单独完成这项工程需要60天,若由甲队先做20天,剩下的工程由甲、乙合作24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,且关于
的图象如图所示,且关于![]() 的一元二次方程
的一元二次方程![]() 没有实数根,有下列结论:①
没有实数根,有下列结论:①![]() ②
②![]() ③
③![]() ④
④![]() 其中,正确的是结论的个数是( )
其中,正确的是结论的个数是( )
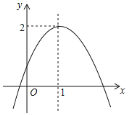
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 切
切![]() 于点
于点![]() ,
,![]() ,
,![]() 是
是![]() 半径的
半径的![]() 倍.
倍.
![]() 求
求![]() 的半径
的半径![]() ;
;
![]() 如图
如图![]() ,弦
,弦![]() ,动点
,动点![]() 从
从![]() 出发沿直径
出发沿直径![]() 向
向![]() 运动的过程中,图中阴影部分的面积是否发生变化,若发生变化,请你说明理由;若不发生变化,请你求出阴影部分的面积;
运动的过程中,图中阴影部分的面积是否发生变化,若发生变化,请你说明理由;若不发生变化,请你求出阴影部分的面积;
![]() 如图
如图![]() ,动点
,动点![]() 从
从![]() 出发,在
出发,在![]() 上按逆时针方向向
上按逆时针方向向![]() 运动.连接
运动.连接![]() ,过
,过![]() 作
作![]() 的垂线,与
的垂线,与![]() 的延长线交于点
的延长线交于点![]() ,当点
,当点![]() 运动到什么位置时,
运动到什么位置时,![]() 取到最大值?求此时动点
取到最大值?求此时动点![]() 所经过的弧长.
所经过的弧长.
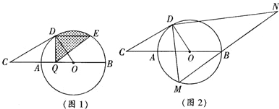
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com