【题目】如图所示，有一座拱桥圆弧形，它的跨度
为
米，拱高为
米，当洪水泛滥到跨度只有
米时，就要采取紧急措施，若拱顶离水面只有
米，即
米时，试通过计算说明是否需要采取紧急措施？
【答案】不用采取紧急措施．
【解析】
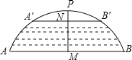
连接OA′，OA．设圆的半径是R，则ON=R﹣4，OM=R﹣18．根据垂径定理求得AM的长，在直角三角形AOM中，根据勾股定理求得R的值，在直角三角形A′ON中，根据勾股定理求得A′N的值，再根据垂径定理求得A′B′的长，从而作出判断．
设O为弧AB所在圆的圆心，连接OA′，OA．设圆的半径是R，则ON=（R﹣4）米，OM=（R﹣18）．
根据垂径定理，得AM=
AB=30，在直角三角形AOM中，∵AO=R，AM=30，OM=（R﹣18），根据勾股定理，得：R2=（R﹣18）2+900，解得：R=34．
在直角三角形A′ON中，根据勾股定理得：A′N=
=16．
根据垂径定理，得：A′B′=2A′N=32＞30，∴不用采取紧急措施．
科目：初中数学 来源： 题型：
【题目】平面直角坐标系xOy中，横坐标为a的点A在反比例函数y1═
（x＞0）的图象上，点A′与点A关于点O对称，一次函数y2=mx+n的图象经过点A′．
（1）设a=2，点B（4，2）在函数y1、y2的图象上．
①分别求函数y1、y2的表达式；
②直接写出使y1＞y2＞0成立的x的范围；
（2）如图①，设函数y1、y2的图象相交于点B，点B的横坐标为3a，△AA'B的面积为16，求k的值；
（3）设m=
，如图②，过点A作AD⊥x轴，与函数y2的图象相交于点D，以AD为一边向右侧作正方形ADEF，试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，AB=AC，D是线段BC的延长线上一点，以AD为一边在AD的右侧作△ADE，使AE=AD，∠DAE=∠BAC，连接CE．
（1）如图1，点D在线段BC的延长线上移动，若∠BAC=30°，则∠DCE= ．
（2）设∠BAC=α，∠DCE=β：
①如图1，当点D在线段BC的延长线上移动时，α与β之间有什么数量关系？请说明理由；
②当点D在直线BC上（不与B、C重合）移动时，α与β之间有什么数量关系？请直接写出你的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数
的图象分别交
轴、
轴于点
、点
，与反比例函数
的图象在第四象限的相交于点
，并且
轴于点
，
轴于点
，已知
，且
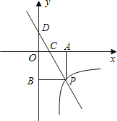
求上述一次函数与反比例函数的表达式；
求一次函数与反比例函数的另一个交点坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某市教育行政部门为了解初三学生每学期参加综合实践活动的情况，随机抽样调查了某校初三学生一个学期参加综合实践活动的天数，并用得到的数据绘制了下面两幅不完整的统计图（如图）.请你根据图中提供的信息，回答下列问题：
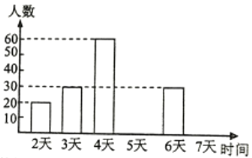
（1）该校初三学生总数为 人；
（2）分别求出活动时间为5天、7天的学生人数为 、 ，并补全频数分布直方图；
（3）扇形统计图中“活动时间为5天”的扇形所对圆心角的度数是 ；
（4）在这次抽样调查中，众数和中位数分别是 、 ；
（5）如果该市共有初三学生96000人，请你估计“活动时间不少于5天”的大约有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某西瓜经营户以
元/千克的价格购进一批小型西瓜，以
元/千克的价格出售，每天可售出
千克．为了促销，该经营户决定降价销售．经调查发现，这种小型西瓜每降价
元/千克，每天可多售出
千克．另外，每天的房租等固定成本共
元．该经营户要想每天盈利元，应将每千克小型西瓜的售价降低________元．
查看答案和解析>>
科目：初中数学 来源： 题型：
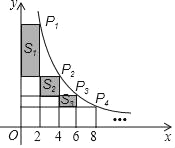
【题目】如图，在反比例函数y=
（x＞0）的图象上，有点P1，P2，P3，P4，…，它们的横坐标依次为2，4，6，8，…分别过这些点作x轴与y轴的垂线，图中所构成的阴影部分的面积从左到右依次记为S1，S2，S3，…，Sn，则S1+S2+S3+…+Sn=_____（用含n的代数式表示）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC中，AB=2，AC=3，1＜BC＜5，分别以AB、BC、AC为边向外作正方形ABIH、BCDE和正方形ACFG，则图中阴影部分的最大面积为（ ）
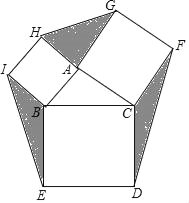
A. 6 B. 9 C. 11 D. 无法计算
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在平面直角坐标系中△ABC三个顶点的坐标分别是点A(﹣2，3)、点B(﹣1，1)、点C(0，2)．
（1）作△ABC关于C成中心对称的△A1B1C1；
（2）将△A1B1C1向右平移3个单位，作出平移后的△A2B2C2；
（3）在x轴上求作一点P，使PA1+PC1的值最小，并写出点 P 的坐标．（不写解答过程，直接写出结果）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com