
【题目】某市教育行政部门为了解初三学生每学期参加综合实践活动的情况,随机抽样调查了某校初三学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图).请你根据图中提供的信息,回答下列问题:

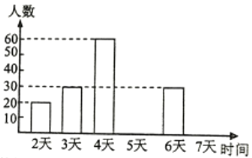
(1)该校初三学生总数为 人;
(2)分别求出活动时间为5天、7天的学生人数为 、 ,并补全频数分布直方图;
(3)扇形统计图中“活动时间为5天”的扇形所对圆心角的度数是 ;
(4)在这次抽样调查中,众数和中位数分别是 、 ;
(5)如果该市共有初三学生96000人,请你估计“活动时间不少于5天”的大约有多少人?
【答案】(1)200;(2)50,10;图见解析;(3)![]() ;(4)4天,4天;(5)
;(4)4天,4天;(5)![]() (人)
(人)
【解析】
(1)活动时间为2天的人数除以百分比,即可求解;
(2)抽取的人数乘以活动时间为5天和7天的百分比,即可求解;
(3)360°乘以活动时间为5天的百分比,即可求解;
(4)根据众数,中位数的定义,即可求解;
(5)96000乘以活动时间为5天,6天,7天的百分比之和,即可求解.
(1)20÷0.1=200(人),
答:该校初三学生总数为200人.
故答案是:200;
(2)200×0.05=10(人),200×(1-0.15-0.05-0.1-0.15-0.3)=50(人),
答:活动时间为5天、7天的学生人数分别为:50人,10人.
故答案是:50,10;
频数直方图,如图所示:
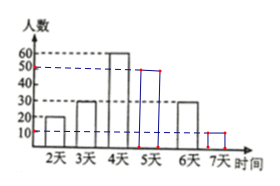
(3)360°×0.25=90°,
答:扇形统计图中“活动时间为5天”的扇形所对圆心角的度数是90°.
故答案是:90°;
(4)∵活动时间为4天的人数最多,
∴众数是:4天,
∵总人数为200人,按活动时间从小到大排序,第100,101人的活动天数都是4天,
∴中位数是:4天.
故答案是:4天,4天;
(5)96000×(0.05+0.15+0.25)=![]() (人),
(人),
答:估计“活动时间不少于5天”的大约有多少人.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 以上均不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年暑假,都有许多驴友为实现自己的一个梦想,骑自行车丈量中国最美的公路川藏线。![]() 、
、![]() 两个驴友团队于同一天出发前往目的地拉萨。
两个驴友团队于同一天出发前往目的地拉萨。![]() 队走317国道,结果30天到达。
队走317国道,结果30天到达。![]() 队走318国道,总路程比
队走318国道,总路程比![]() 队少200千米,且路况更好,平均每天比
队少200千米,且路况更好,平均每天比![]() 队多骑行20千米,结果
队多骑行20千米,结果![]() 队比
队比![]() 队提前8天到达拉萨.
队提前8天到达拉萨.
(1)求318国道全程为多少千米?
(2)骑行过程中,![]() 队每人每天平均花费150元。
队每人每天平均花费150元。![]() 队开始有3个人同行,计划每人每天花费110元,后来又有几个人加入队伍,实际每增加1人时,每人每天的平均花费就减少5元。若最终
队开始有3个人同行,计划每人每天花费110元,后来又有几个人加入队伍,实际每增加1人时,每人每天的平均花费就减少5元。若最终![]() 、
、![]() 两队骑行的人数相同(均不超过10人),两队共花费了36900元,求两驴友团队各有多少人?
两队骑行的人数相同(均不超过10人),两队共花费了36900元,求两驴友团队各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要使△ABD≌△ACD,需从下列条件中增加一个,错误的选法是( )

A.∠ADB=∠ADCB.∠B=∠CC.AB=ACD.DB=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知图中的曲线是反比例函数![]() 为常数,
为常数,![]() 图象的一支.
图象的一支.
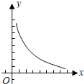
![]() 这个反比例函数图象的另一支在第几象限?常数
这个反比例函数图象的另一支在第几象限?常数![]() 的取值范围是什么;
的取值范围是什么;
![]() 若该函数的图象与正比例函数
若该函数的图象与正比例函数![]() 的图象在第一象内限的交点为
的图象在第一象内限的交点为![]() ,过
,过![]() 点作
点作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,当
,当![]() 的面积为
的面积为![]() 时,求点
时,求点![]() 的坐标及反比例函数的解析式.
的坐标及反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
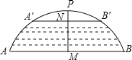
【题目】如图所示,有一座拱桥圆弧形,它的跨度![]() 为
为![]() 米,拱高为
米,拱高为![]() 米,当洪水泛滥到跨度只有
米,当洪水泛滥到跨度只有![]() 米时,就要采取紧急措施,若拱顶离水面只有
米时,就要采取紧急措施,若拱顶离水面只有![]() 米,即
米,即![]() 米时,试通过计算说明是否需要采取紧急措施?
米时,试通过计算说明是否需要采取紧急措施?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中有三点![]() 、
、![]() 、
、![]() .请回答如下问题:
.请回答如下问题:
(1)在坐标系内描出![]() ;
;
(2)在坐标系中画出![]() ,使它与
,使它与![]() 关于
关于![]() 轴对称;
轴对称;
(3)在![]() 轴上找一点
轴上找一点![]() ,使
,使![]() 的值最小,并求出此最小值.
的值最小,并求出此最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两位同学用围棋子做游戏.如图所示,现轮到黑棋下子,黑棋下一子后白棋再下一子,使黑棋的5个棋子组成轴对称图形,白棋的5个棋子也成轴对称图形.则下列下子方法不正确的是【 】.[说明:棋子的位置用数对表示,如A点在(6,3)]

A.黑(3,7);白(5,3) B.黑(4,7);白(6,2)
C.黑(2,7);白(5,3) D.黑(3,7);白(2,6)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com