
【题目】(9分)已知:![]() ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么![]() ABCD的周长是多少?
ABCD的周长是多少?
【答案】解:(1)∵四边形ABCD是菱形,∴AB=AD。
又∵![]() ,
,
当![]() ,即m=1时,四边形ABCD是菱形。
,即m=1时,四边形ABCD是菱形。
把m=1代入![]() ,得
,得![]() 。
。
∴![]() 。
。
∴菱形ABCD的边长是![]() 。
。
(2)把AB=2代入![]() ,得
,得![]() ,解得
,解得![]() 。
。
把![]() 代入
代入![]() ,得
,得![]() 。
。
解得![]() ,
,![]() 。∴AD=
。∴AD=![]() 。
。
∵四边形ABCD是平行四边形,
∴□ABCD的周长是2(2+![]() )=5。
)=5。
【解析】
(1)根据菱形的性质可得出AB=AD,由根的判别式即可得出关于m的一元二次方程,解之即可得出m的值;
(2)将x=2代入一元二次方程可求出m的值,再根据根与系数的关系即可得出AB+AD的值,利用平行四边形的性质即可求出平行四边形ABCD的周长.
解:(1)∵四边形ABCD是菱形,
∴AB=AD,
∵AB、AD的长是关于x的一元二次方程x2﹣mx+![]() =0的两个实数根,
=0的两个实数根,
∴△=(﹣m)2﹣4(![]() )=m2﹣2m+1=0,
)=m2﹣2m+1=0,
解得:m=1.
∴当m为1时,四边形ABCD是菱形.
(2)将x=2代入x2﹣mx+![]() =0中,得:4﹣2m+
=0中,得:4﹣2m+![]() =0,
=0,
解得:m=![]() ,
,
∵AB、AD的长是关于x的一元二次方程x2﹣mx+![]() =0的两个实数根,
=0的两个实数根,
∴AB+AD=m=![]() ,
,
∴平行四边形ABCD的周长=2(AB+AD)=2×![]() =5.
=5.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理,如图所示的矩形由两个这样的图形拼成,若a=3,b=4,则该矩形的面积为( )

A. 20 B. 24 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克![]() 元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克
元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克![]() 元,经试销发现,销售量
元,经试销发现,销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)符合一次函数关系,如图是
(元)符合一次函数关系,如图是![]() 与
与![]() 的函数关系图象.
的函数关系图象.
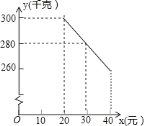
![]() 求
求![]() 与
与![]() 的函数解析式(也称关系式);
的函数解析式(也称关系式);
![]() 设该水果销售店试销草莓获得的利润为
设该水果销售店试销草莓获得的利润为![]() 元,求
元,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:x2﹣6x=(x2﹣6x+9)﹣9=(x﹣3)2﹣9;﹣x2+10=﹣(x2﹣10x+25)+25=﹣(x﹣5)2+25,这一种方法称为配方法,利用配方法请解以下各题:
(1)按上面材料提示的方法填空:a2﹣4a= = .﹣a2+12a= = .
(2)探究:当a取不同的实数时在得到的代数式a2﹣4a的值中是否存在最小值?请说明理由.
(3)应用:如图.已知线段AB=6,M是AB上的一个动点,设AM=x,以AM为一边作正方形AMND,再以MB、MN为一组邻边作长方形MBCN.问:当点M在AB上运动时,长方形MBCN的面积是否存在最大值?若存在,请求出这个最大值;否则请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出 4台.商场要想在这种冰箱销售中每天盈利 4800 元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)如图1,求证:矩形DEFG是正方形;
(2)若AB=2,CE=![]() ,求CG的长度;
,求CG的长度;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:AB是⊙O的直径,点C在⊙O上,CD是⊙O的切线,AD⊥CD于点D.E是AB延长线上一点,CE交⊙O于点F,连结OC,AC.

(1)求证:AC平分∠DAO;
(2)若∠DAO=105°,∠E=30°.①求∠OCE的度数.②若⊙O的半径为![]() ,求线段EF的长.
,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平面直角坐标系中,已知![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() ,
,![]() ,
,![]() .
.
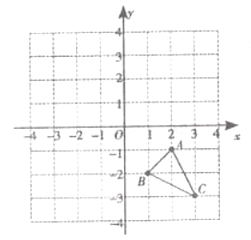
(1)将![]() 向上平移
向上平移![]() 个单位长度,再向左平移
个单位长度,再向左平移![]() 个单位长度,得到
个单位长度,得到![]() ,请画出
,请画出![]() (点
(点![]() ,
,![]() ,
,![]() 的对应点分别为
的对应点分别为![]() ,
,![]() ,
,![]() )
)
(2)请画出与![]() 关于
关于![]() 轴对称的
轴对称的![]() (点
(点![]() ,
,![]() ,
,![]() 的对应点分别为
的对应点分别为![]() ,
,![]() ,
,![]() )
)
(3)请写出![]() ,
,![]() 的坐标
的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
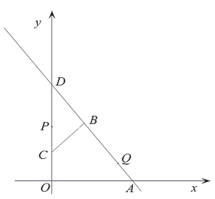
【题目】如图,在平面直角坐标系中,已知点A的坐标为(15,0),点B的坐标为(6,12),点C的坐标为(0,6), 直线AB交y轴于点D, 动点P从点C出发沿着y轴正方向以每秒2个单位的速度运动, 同时,动点Q从点A出发沿着射线AB以每秒a个单位的速度运动设运动时间为t秒,
(1)求直线AB的解析式和CD的长.
(2)当△PQD与△BDC全等时,求a的值.
(3)记点P关于直线BC的对称点为![]() ,连结
,连结![]() 当t=3,
当t=3,![]() 时, 求点Q的坐标.
时, 求点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com