
【题目】(1)问题发现
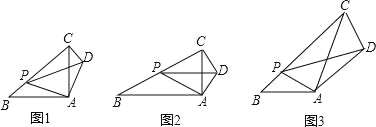
如图1,在Rt△ABC中,∠A=90°,![]() =1,点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接 CD.
=1,点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接 CD.
(1)①求![]() 的值;②求∠ACD的度数.
的值;②求∠ACD的度数.
(2)拓展探究
如图 2,在Rt△ABC中,∠A=90°,![]() =k.点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接CD,请判断∠ACD与∠B 的数量关系以及PB与CD之间的数量关系,并说明理由.
=k.点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接CD,请判断∠ACD与∠B 的数量关系以及PB与CD之间的数量关系,并说明理由.
(3)解决问题
如图 3,在△ABC中,∠B=45°,AB=4![]() ,BC=12,P 是边BC上一动点(不与点B重合),∠PAD=∠BAC,∠APD=∠B,连接CD.若 PA=5,请直接写出CD的长.
,BC=12,P 是边BC上一动点(不与点B重合),∠PAD=∠BAC,∠APD=∠B,连接CD.若 PA=5,请直接写出CD的长.
【答案】(1)1,45°;(2)∠ACD=∠B,![]() =k;(3)
=k;(3)![]() .
.
【解析】
(1)根据已知条件推出△ABP≌△ACD,根据全等三角形的性质得到PB=CD,∠ACD=∠B=45°,于是得到 ![]()
![]() 根据已知条件得到△ABC∽△APD,由相似三角形的性质得到
根据已知条件得到△ABC∽△APD,由相似三角形的性质得到![]() ,得到 ABP∽△CAD,根据相似三角形的性质得到结论;
,得到 ABP∽△CAD,根据相似三角形的性质得到结论;
![]() 过A作AH⊥BC 于 H,得到△ABH 是等腰直角三角形,求得 AH=BH=4, 根据勾股定理得到
过A作AH⊥BC 于 H,得到△ABH 是等腰直角三角形,求得 AH=BH=4, 根据勾股定理得到![]() 根据相似三角形的性质得到
根据相似三角形的性质得到 ![]() ,推出△ABP∽△CAD,根据相似三角形的性质即可得到结论.
,推出△ABP∽△CAD,根据相似三角形的性质即可得到结论.
(1)∵∠A=90°,
![]()
∴AB=AC,
∴∠B=45°,
∵∠PAD=90°,∠APD=∠B=45°,
∴AP=AD,
∴∠BAP=∠CAD,
在△ABP 与△ACD 中,
AB=AC, ∠BAP=∠CAD,AP=AD,
∴△ABP≌△ACD,
∴PB=CD,∠ACD=∠B=45°,
∴![]() =1,
=1,
(2)![]()
∵∠BAC=∠PAD=90°,∠B=∠APD,
∴△ABC∽△APD,
![]()
∵∠BAP+∠PAC=∠PAC+∠CAD=90°,
∴∠BAP=∠CAD,
∴△ABP∽△CAD,
∴∠ACD=∠B,
![]()
(3)过 A 作 AH⊥BC 于 H,
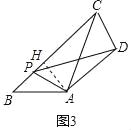
∵∠B=45°,
∴△ABH 是等腰直角三角形,
∵![]()
∴AH=BH=4,
∵BC=12,
∴CH=8,
∴![]()
∴PH=![]() =3,
=3,
∴PB=1,
∵∠BAC=∠PAD=,∠B=∠APD,
∴△ABC∽△APD,
∴![]() ,
,
∵∠BAP+∠PAC=∠PAC+∠CAD,
∴∠BAP=∠CAD,
∴△ABP∽△CAD,
∴![]() 即
即![]()
∴![]()
过 A 作 AH⊥BC 于 H,
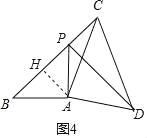
∵∠B=45°,
∴△ABH 是等腰直角三角形,
∵![]()
∴AH=BH=4,
∵BC=12,
∴CH=8,
∴![]()
∴PH=![]() =3,
=3,
∴PB=7,
∵∠BAC=∠PAD=,∠B=∠APD,
∴△ABC∽△APD,
∴![]() ,
,
∵∠BAP+∠PAC=∠PAC+∠CAD,
∴∠BAP=∠CAD,
∴△ABP∽△CAD,
∴![]() 即
即![]()
∴![]()


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”是我们倡导的一种生活方式,有关部门抽样调查了某单位员工上下班的交通方式,绘制了两幅统计图:
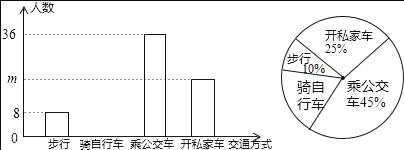
(1)样本中的总人数为 人;扇形统计十图中“骑自行车”所在扇形的圆心角为 度;
(2)补全条形统计图;
(3)该单位共有1000人,积极践行这种生活方式,越来越多的人上下班由开私家车改为骑自行车.若步行,坐公交车上下班的人数保持不变,问原来开私家车的人中至少有多少人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下的题目:如图1,在等边![]() 中,点
中,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,试确定线段
,试确定线段![]() 与
与![]() 的大小关系,并说明理由,
的大小关系,并说明理由,
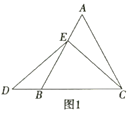
(1)小敏与同桌小聪探究解答的思路如下:
①特殊情况,探索结论,
当点![]() 为
为![]() 的中点时,如图2,确定线段
的中点时,如图2,确定线段![]() 与
与![]() 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论:![]() ______
______![]() .(填>,<或=)
.(填>,<或=)
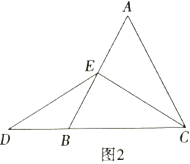
②特例启发,解答题目,
解:题目中,![]() 与
与![]() 的大小关系是:
的大小关系是:![]() ______
______![]() .(填>,<或=)
.(填>,<或=)
理由如下:如图3,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,(请你补充完成解答过程)
,(请你补充完成解答过程)
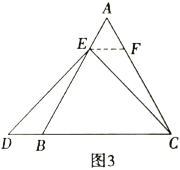
(2)拓展结论,设计新题,
同学小敏解答后,提出了新的问题:在等边![]() 中,点
中,点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 上,且
上,且![]() ,已知
,已知![]() 的边长为
的边长为![]() ,求
,求![]() 的长?(请直接写出结果)
的长?(请直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为![]() ,
,![]() ,
,![]() ,用记号
,用记号![]() 表示一个满足条件的三角形,如
表示一个满足条件的三角形,如![]() 表示边长分别为2,4,4个单位长度的一个三角形.
表示边长分别为2,4,4个单位长度的一个三角形.
(1)若这些三角形三边的长度为大于0且小于3的整数个单位长度,请用记号写出所有满足条件的三角形;
(2)如图,![]() 是
是![]() 的中线,线段
的中线,线段![]() ,
,![]() 的长度分别为2个,6个单位长度,且线段
的长度分别为2个,6个单位长度,且线段![]() 的长度为整数个单位长度,过点
的长度为整数个单位长度,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]()
①求![]() 之长;
之长;
②请直接用记号表示![]() .
.
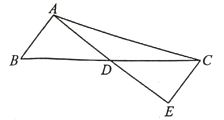
查看答案和解析>>
科目:初中数学 来源: 题型:
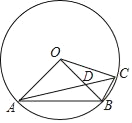
【题目】如图,⊙O是△ABC的外接圆,OA=2cm,OA⊥OB,AC交OB于D点,AD=2CD.
(1)求∠BOC的度数;
(2)求线段BD、线段CD和 BC围成的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为厉行节能减排,倡导绿色出行,今年3月以来.“共享单车”(俗称“小黄车”)公益活动登陆我市中心城区,某公司拟在甲、乙两个街道社区投放一批“小黄车”,这批自行车包括A、B两种不同款型,请回答下列问题:
问题1:单价
该公司早期在甲街区进行了试点投放,共投放A、B两型自行车各50辆,投放成本共计7500元,其中B型车的成本单价比A型车高10元,A、B两型自行车的单价各是多少?
问题2:投放方式
该公司决定采取如下投放方式:甲街区每1000人投放a辆“小黄车”,乙街区每1000人投放![]() 辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 上运动(不与点
上运动(不与点![]() 重合).
重合).
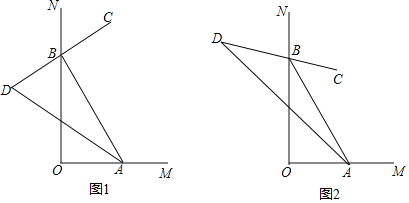
(1)如图1,![]() 是
是![]() 的平分线,
的平分线,![]() 的反方向延长线与
的反方向延长线与![]() 的平分线交于点
的平分线交于点![]() .
.
①若![]() ,则
,则![]() 为多少度?请说明理由.
为多少度?请说明理由.
②猜想:![]() 的度数是否随
的度数是否随![]() 、
、![]() 的移动发生变化?请说明理由.
的移动发生变化?请说明理由.
(2)如图2,若![]() ,
,![]() ,则
,则![]() 的大小为 度(直接写出结果);
的大小为 度(直接写出结果);
(3)若将“![]() ”改为“
”改为“![]() (
(![]() )”,且
)”,且![]() ,
,![]() ,其余条件不变,则
,其余条件不变,则![]() 的大小为 度(用含
的大小为 度(用含![]() 、
、![]() 的代数式直接表示出米).
的代数式直接表示出米).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com