
����Ŀ������̼�����ɫ�����������dz�����һ�����ʽ���йز��ų���������ij��λԱ�����°�Ľ�ͨ��ʽ������������ͳ��ͼ��
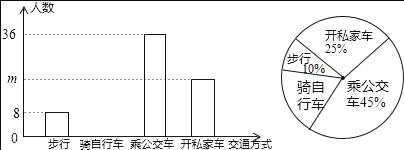
��1�������е�������Ϊ�����ˣ�����ͳ��ʮͼ���������г����������ε�Բ�Ľ�Ϊ�����ȣ�
��2����ȫ����ͳ��ͼ��
��3���õ�λ����1000�ˣ����������������ʽ��Խ��Խ��������°��ɿ�˽�ҳ���Ϊ�����г��������У������������°���������ֲ��䣬��ԭ����˽�ҳ������������ж����˸�Ϊ�����г�������ʹ�����г������������ڿ�˽�ҳ���������
���𰸡�(1) 80��72��(2) 16��;(3) 50��
��������
(1) �ò���������������ռ�İٷֱȼ��ɵõ�����������:8![]() 10%=80(��);�����������Կ�˽�ҳ�����ռ�ٷֱȼ������������ m=80
10%=80(��);�����������Կ�˽�ҳ�����ռ�ٷֱȼ������������ m=80![]() 25%=20;��3600���������г���ռ�İٷֱȼ���������������ε�Բ�Ľ�:360
25%=20;��3600���������г���ռ�İٷֱȼ���������������ε�Բ�Ľ�:360![]() (1-10%-25%-45%)=
(1-10%-25%-45%)=![]() .
.
(2) ��������ͳ��ͼ��������г�����ռ�ٷֱ�, �������������Ըðٷֱȼ�����������г�������, ��ȫ����ͼ���ɣ�
(3) ��������ԭ����˽�ҳ���������x�˸�Ϊ�����г�, ��x�ֱ��ʾ�ı���з�ʽ��������г��Ϳ�˽�ҳ�������, ���������г�һԪһ�β���ʽ, �ⲻ��ʽ���ɣ�
�⣺��1�������е�������Ϊ8��10%=80�ˣ�
�������г��İٷֱ�Ϊ1����10%+25%+45%��=20%��
������ͳ��ʮͼ���������г����������ε�Բ�Ľ�Ϊ360���20%=72��
��2�������г�������Ϊ80��20%=16�ˣ�
��ȫͼ�����£�
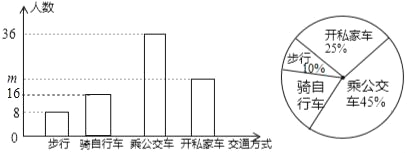
��3����ԭ����˽�ҳ���������x�˸������г���
�����⣬�ã�1000����1��10%��25%��45%��+x��1000��25%��x��
��ã�x��50��
��ԭ����˽�ҳ�������������50�˸�Ϊ�����г�������ʹ�����г������������ڿ�˽�ҳ���������


 ��ĩ�óɼ�ϵ�д�
��ĩ�óɼ�ϵ�д� 99��1������ĩ��ѵ��ϵ�д�
99��1������ĩ��ѵ��ϵ�д� ��ǿ��У��ĩ���100��ϵ�д�
��ǿ��У��ĩ���100��ϵ�д� �óɼ�1��1��ĩ���100��ϵ�д�
�óɼ�1��1��ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
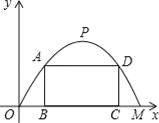
����Ŀ��ʩ����Ҫ��һ�������Ϊ�����ߵĹ�·��������߶�Ϊ6�ף�����OMΪ12�ף�����O��Ϊԭ�㣬OM����ֱ��Ϊx�Ὠ��ֱ������ϵ����ͼ��ʾ����
��1��ֱ��д����M�������߶���P�����ꣻ
��2��������������ߵĺ�������ʽ��
��3��ʩ���Ӽƻ��������ſڴһ�����������ּ���ABCD��ʹA��D�����������ϣ�B��C���ڵ���OM�ϣ�Ϊ�˳ﱸ���ϣ�����������ּ�������ľ��AB��AD��DC�ij���֮�͵����ֵ�Ƕ��٣������ʩ���Ӽ���һ�£�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
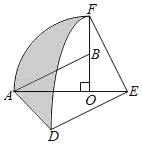
����Ŀ����ͼ����Rt��AOB�У���AOB=90�㣬OA=2��OB=1����Rt��AOB�Ƶ�O˳ʱ����ת90����õ�Rt��FOE�����߶�EF�Ƶ�E��ʱ����ת90����õ��߶�ED���քe��O��EΪԲ�ģ�OA��ED��Ϊ�뾶����AF�ͻ�DF������AD����ͼ����Ӱ���ֵ������__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AD=2��AB=3������A��C�����Ϊ2��ƽ���߶�AE��CF���ֱ�CD��AB�ڵ�E��F����DE�ij��ǣ�������

A. ![]() B.
B. ![]() C. 1 D.
C. 1 D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ת��������ѧ�е�һ����Ҫ˼�룬����İ��������ת������Ϥ�����⣬�Ѹ��ӵ�����ת���ɼ����⣬�ѳ��������ת��Ϊ��������⣮
��1����������Ѿ�ѧ����֪ʶ�����������ͼ��1���С�A+��B+��C+��D+��E�Ķ�����
��2������ͼ��1�������ν�ȥһ���ǣ���ͼ��2�������������A+��B+��C+��D+��E+��F�Ķ�����
��3�����ٶ�ͼ��2���еĽǽ�һ����ȥ���������⣨2�������õķ�������ɣ�����ͼ3�еġ�A+��B+��C+��D+��E+��F+��G+��H+��M+��N�Ķ�����ֻҪд�����ۣ�����Ҫд��������̣�
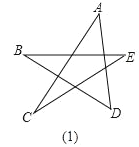
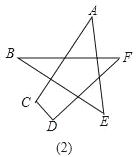
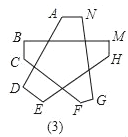
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��MP��NQ�ֱ�ֱƽ��AB��AC.
(1)����APQ���ܳ�Ϊ12����BC�ij���
(2)��BAC��105�������PAQ�Ķ�����
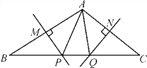
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
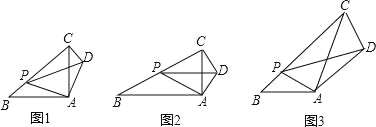
����Ŀ����1�����ⷢ��
��ͼ1����Rt��ABC�У���A=90�㣬![]() =1����P�DZ�BC��һ���㣨�����B�غϣ�����PAD=90�㣬��APD=��B������ CD��
=1����P�DZ�BC��һ���㣨�����B�غϣ�����PAD=90�㣬��APD=��B������ CD��
��1������![]() ��ֵ�������ACD�Ķ�����
��ֵ�������ACD�Ķ�����
��2����չ̽��
��ͼ 2����Rt��ABC�У���A=90�㣬![]() =k����P�DZ�BC��һ���㣨�����B�غϣ�����PAD=90�㣬��APD=��B������CD�����жϡ�ACD���B ��������ϵ�Լ�PB��CD֮���������ϵ����˵�����ɣ�
=k����P�DZ�BC��һ���㣨�����B�غϣ�����PAD=90�㣬��APD=��B������CD�����жϡ�ACD���B ��������ϵ�Լ�PB��CD֮���������ϵ����˵�����ɣ�
��3���������
��ͼ 3���ڡ�ABC�У���B=45�㣬AB=4![]() ��BC=12��P �DZ�BC��һ���㣨�����B�غϣ�����PAD=��BAC����APD=��B������CD���� PA=5����ֱ��д��CD�ij���
��BC=12��P �DZ�BC��һ���㣨�����B�غϣ�����PAD=��BAC����APD=��B������CD���� PA=5����ֱ��д��CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
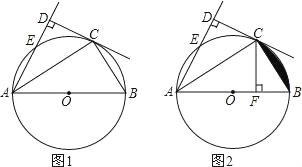
����Ŀ����ͼ��ABΪ��O��ֱ����C��EΪO�ϵ����㣬��ACƽ�֡�EAB��CD��AE�ڵ�D��
��1����֤��DC�ǡ�O���ߣ�
��2����AO��6��DC��3![]() ����DE�ij���
����DE�ij���
��3������C��CF��AB��F����ͼ2����AD��OA��1.5��AC��3![]() ����ͼ����Ӱ���������
����ͼ����Ӱ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ��ȤС���ڡ��������֤ƽ���ʽ��ʱ�����������µ�̽�����̣�
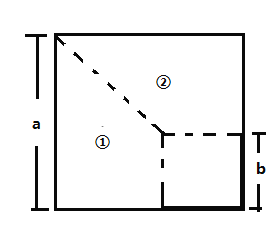
��1��С�����뷨�ǣ����߳�Ϊ![]() �����������½Ǽ���һ���߳�Ϊ
�����������½Ǽ���һ���߳�Ϊ![]() ��������(��ͼ1)����ʣ�²��ְ������߷ָ�ɢٺ͢������֣��������ַ�ʽ��ʾ������������ĺͣ����㰴��С�����뷨��֤ƽ���ʽ��
��������(��ͼ1)����ʣ�²��ְ������߷ָ�ɢٺ͢������֣��������ַ�ʽ��ʾ������������ĺͣ����㰴��С�����뷨��֤ƽ���ʽ��
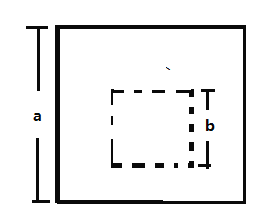
��2��С���뷨�ǣ��ڱ߳�Ϊ![]() ���������ڲ�����λ�ü���һ���߳�Ϊ
���������ڲ�����λ�ü���һ���߳�Ϊ![]() ��������(��ͼ2)���ٽ�ʣ�²��ֽ����ʵ��ָ�����ָ�õ��ļ���������������ַ�ʽ��ʾ���������㰴��С���뷨��ͼ�����������ָ��ߣ�����֤ƽ���ʽ��
��������(��ͼ2)���ٽ�ʣ�²��ֽ����ʵ��ָ�����ָ�õ��ļ���������������ַ�ʽ��ʾ���������㰴��С���뷨��ͼ�����������ָ��ߣ�����֤ƽ���ʽ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com