
【题目】如图,AB为⊙O的直径,C,E为O上的两点,若AC平分∠EAB,CD⊥AE于点D.
(1)求证:DC是⊙O切线;
(2)若AO=6,DC=3![]() ,求DE的长;
,求DE的长;
(3)过点C作CF⊥AB于F,如图2,若AD﹣OA=1.5,AC=3![]() ,求图中阴影部分面积.
,求图中阴影部分面积.
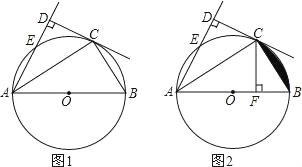
【答案】(1)证明见解析;(2)3;(3)![]()
【解析】
(1)连接OC,如图1,先证明∠1=∠3得到OC∥AD,再利用平行线的性质得OC⊥CD,然后根据切线的判定定理得到结论;
(2)连接BE交OC于H,如图1,利用圆周角定理得∠AEB=90°,易得四边形CDEH为矩形,则CD=EH=3![]() ,CH=ED,利用垂径定理得BH=3
,CH=ED,利用垂径定理得BH=3![]() ,然后利用勾股定理计算出OH后计算出CH,从而得到DE的长;
,然后利用勾股定理计算出OH后计算出CH,从而得到DE的长;
(3)连接OC,如图2,设⊙O的半径为r,利用角平分线的性质得CD=CF,则根据勾股定理得AD=AF,于是可计算出OF=1.5,再证明△ACF∽△ABC,利用相似比得到![]() ,解得r=3,接着在Rt△OCF中利用解直角三角形得到∠COF=60°,CF=
,解得r=3,接着在Rt△OCF中利用解直角三角形得到∠COF=60°,CF=![]() ,然后根据扇形面积公式,利用图中阴影部分面积=S扇形BOC-S△OCB进行计算.
,然后根据扇形面积公式,利用图中阴影部分面积=S扇形BOC-S△OCB进行计算.
(1)连接OC,如图1,
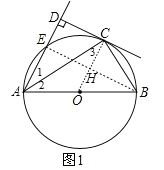
∵AC平分∠EAB,
∴∠1=∠2,
∵OA=OC,
∴∠2=∠3,
∴∠1=∠3,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
∴DC是⊙O切线;
(2)连接BE交OC于H,如图1,
∵AB为⊙O的直径,
∴∠AEB=90°,
∵OC∥AD,
∴∠OHB=90°,
∴EH=BH,四边形CDEH为矩形,
∴CD=EH=3![]() ,CH=ED,
,CH=ED,
∴BH=3![]() ,
,
在Rt△OBH中,OH=![]() =3,
=3,
∴CH=6-3=3,
∴DE=3;
(3)连接OC,如图2,设⊙O的半径为r,
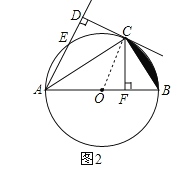
∵AC平分∠BAD,CD⊥AD,CF⊥AB,
∴CD=CF,
∴AD=AF=AO+OF,
∵AD-OA=1.5,
∴AO+OF-OA=1.5,即OF=1.5,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠CAF=∠BAC,
∴△ACF∽△ABC,
∴![]() ,即
,即![]() ,
,
解得r=-![]() (舍去)或r=3,
(舍去)或r=3,
在Rt△OCF中,cos∠COF=![]() ,
,
∴∠COF=60°,
∴CF=![]() OF=
OF=![]() ,
,
∴图中阴影部分面积=S扇形BOC-S△OCB=![]() -
-![]() ×3×
×3×![]() =
=![]() π-
π-![]() .
.


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】某市为解决部分市民冬季集中取暖问题,需铺设一条长4000米的管道,为尽量减少施工对交通造成的影响,施工时“…”,设实际每天铺设管道x米,则可得方程![]() =20,根据此情景,题中用“…”表示的缺失的条件应补为( )
=20,根据此情景,题中用“…”表示的缺失的条件应补为( )
A. 每天比原计划多铺设10米,结果延期20天完成
B. 每天比原计划少铺设10米,结果延期20天完成
C. 每天比原计划多铺设10米,结果提前20天完成
D. 每天比原计划少铺设10米,结果提前20天完成
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”是我们倡导的一种生活方式,有关部门抽样调查了某单位员工上下班的交通方式,绘制了两幅统计图:
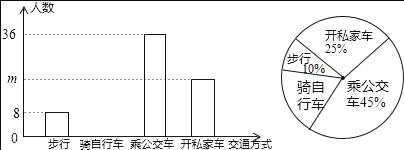
(1)样本中的总人数为 人;扇形统计十图中“骑自行车”所在扇形的圆心角为 度;
(2)补全条形统计图;
(3)该单位共有1000人,积极践行这种生活方式,越来越多的人上下班由开私家车改为骑自行车.若步行,坐公交车上下班的人数保持不变,问原来开私家车的人中至少有多少人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为![]() ,
,![]() ,
,![]() ,用记号
,用记号![]() 表示一个满足条件的三角形,如
表示一个满足条件的三角形,如![]() 表示边长分别为2,4,4个单位长度的一个三角形.
表示边长分别为2,4,4个单位长度的一个三角形.
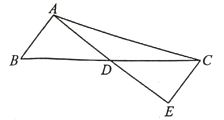
(1)若这些三角形三边的长度为大于0且小于3的整数个单位长度,请用记号写出所有满足条件的三角形;
(2)如图,![]() 是
是![]() 的中线,线段
的中线,线段![]() ,
,![]() 的长度分别为2个,6个单位长度,且线段
的长度分别为2个,6个单位长度,且线段![]() 的长度为整数个单位长度,过点
的长度为整数个单位长度,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]()
①求![]() 之长;
之长;
②请直接用记号表示![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
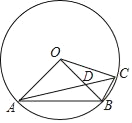
【题目】如图,⊙O是△ABC的外接圆,OA=2cm,OA⊥OB,AC交OB于D点,AD=2CD.
(1)求∠BOC的度数;
(2)求线段BD、线段CD和 BC围成的图形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P的坐标是(a,b),从-2,-1,0,1,2这五个数中任取一个数作为a的值,再从余下的四个数中任取一个数作为b的值,则点P(a,b)在平面直角坐标系中第二象限内的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为厉行节能减排,倡导绿色出行,今年3月以来.“共享单车”(俗称“小黄车”)公益活动登陆我市中心城区,某公司拟在甲、乙两个街道社区投放一批“小黄车”,这批自行车包括A、B两种不同款型,请回答下列问题:
问题1:单价
该公司早期在甲街区进行了试点投放,共投放A、B两型自行车各50辆,投放成本共计7500元,其中B型车的成本单价比A型车高10元,A、B两型自行车的单价各是多少?
问题2:投放方式
该公司决定采取如下投放方式:甲街区每1000人投放a辆“小黄车”,乙街区每1000人投放![]() 辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
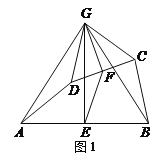
【题目】如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD、BC所在直线互相垂直,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com