
【题目】一个六边形的六个内角都是120°,连续四边的长依次为2.31,2.32,2.33,2.31,则这个六边形的周长为_____.
【答案】13.92
【解析】
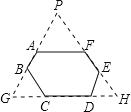
凸六边形ABCDEF,并不是一规则的六边形,但六个角都是120°,所以通过适当的向外作延长线,可得到等边三角形,进而求解.
解:如图,AB=2.31,BC=2.32,CD=2.33,DE=2.31,分别作直线AB、CD、EF的延长线和反向延长线使它们交于点G、H、P.
∵六边形ABCDEF的六个角都是120°,
∴六边形ABCDEF的每一个外角的度数都是60°.
∴△APF、△BGC、△DHE、△GHP都是等边三角形.
∴GC=BC=2.32,DH=DE=2.31.
∴GH=2.32+2.33+2.31=6.96,FA=PA=PG﹣AB﹣BG=6.96﹣2.31﹣2.32=2.33,EF=PH﹣PF﹣EH=6.96﹣2.33﹣2.31=2.32.
∴六边形的周长为2.31+2.32+2.33+2.31+2.32+2.33=13.92.
故答案为:13.92.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )

A. ![]() B.
B. ![]() C. 1 D.
C. 1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
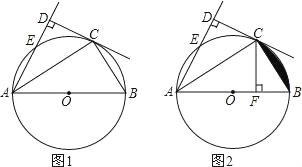
【题目】如图,AB为⊙O的直径,C,E为O上的两点,若AC平分∠EAB,CD⊥AE于点D.
(1)求证:DC是⊙O切线;
(2)若AO=6,DC=3![]() ,求DE的长;
,求DE的长;
(3)过点C作CF⊥AB于F,如图2,若AD﹣OA=1.5,AC=3![]() ,求图中阴影部分面积.
,求图中阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
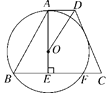
【题目】如图,梯形ABCD中,AD∥BC,AE⊥BC于点E,∠ADC的平分线交AE于点O,以点O为圆心,OA为半径的圆经过点B,交BC于另一点F.
(1)求证:CD与⊙O相切;
(2)若BF=24,OE=5,求tan∠ABC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
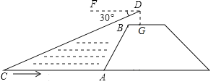
【题目】如图,小黄站在河岸上的![]() 点,看见河里有一小船沿垂直于岸边的方向划过来.此时,测得小船
点,看见河里有一小船沿垂直于岸边的方向划过来.此时,测得小船![]() 的俯角是
的俯角是![]() ,若小黄的眼睛与地面的距离
,若小黄的眼睛与地面的距离![]() 是
是![]() 米,
米,![]() 米,
米,![]() 平行于
平行于![]() 所在的直线,迎水坡
所在的直线,迎水坡![]() 的坡度为
的坡度为![]() ,坡长
,坡长![]() 米,则此时小船
米,则此时小船![]() 到岸边的距离
到岸边的距离![]() 的长为( )米.(
的长为( )米.(![]() ,结果保留两位有效数字)
,结果保留两位有效数字)
A. 11 B. 8.5 C. 7.2 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
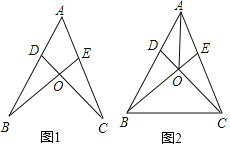
【题目】如图,AE=AD,∠ABE=∠ACD,BE与CD相交于O.
(1)如图1,求证:AB=AC;
(2)如图2,连接BC、AO,请直接写出图2中所有的全等三角形(除△ABE≌△ACD外).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组在“用面积验证平方差公式”时,经历了如下的探究过程;
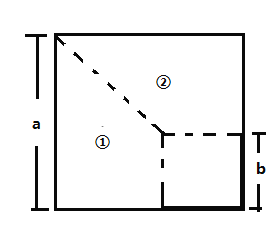
(1)小明的想法是:将边长为![]() 的正方形右下角剪掉一个边长为
的正方形右下角剪掉一个边长为![]() 的正方形(如图1),将剩下部分按照虚线分割成①和②两部分,并用两种方式表示这两部分面积的和,请你按照小明的想法验证平方差公式.
的正方形(如图1),将剩下部分按照虚线分割成①和②两部分,并用两种方式表示这两部分面积的和,请你按照小明的想法验证平方差公式.
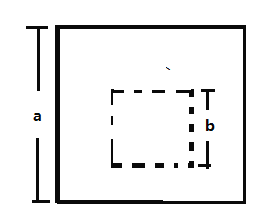
(2)小白的想法是:在边长为![]() 的正方形内部任意位置剪掉一个边长为
的正方形内部任意位置剪掉一个边长为![]() 的正方形(如图2),再将剩下部分进行适当分割,并将分割得到的几部分面积和用两种方式表示出来,请你按照小白的想法在图中用虚线画出分割线,并验证平方差公式.
的正方形(如图2),再将剩下部分进行适当分割,并将分割得到的几部分面积和用两种方式表示出来,请你按照小白的想法在图中用虚线画出分割线,并验证平方差公式.
查看答案和解析>>
科目:初中数学 来源: 题型:
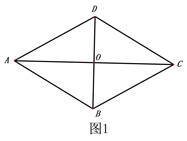
【题目】如图1,菱形ABCD,AB=4,∠ADC=120o,连接对角线AC、BD交于点O,
(1)如图2,将△AOD沿DB平移,使点D与点O重合,求平移后的△A′BO与菱形ABCD重合部分的面积.
(2)如图3,将△A′BO绕点O逆时针旋转交AB于点E′,交BC于点F,
①求证:BE′+BF=2,
②求出四边形OE′BF的面积.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备购进甲、乙两种商品.已知甲商品每件进价15元,售价20元;乙商品每件进价35元,售价45元.
(1)若该商店同时购进甲、乙两种商品共100件,恰好用去2700元,求购进甲、乙两种商品各多少件?
(2)若该商店准备用不超过3100元购进甲、乙两种商品共100件,且这两种商品全部售出后获利不少于890元,问应该怎样进货,才能使总利润最大,最大利润是多少?(利润=售价﹣进价)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com