
【题目】如图,AE=AD,∠ABE=∠ACD,BE与CD相交于O.
(1)如图1,求证:AB=AC;
(2)如图2,连接BC、AO,请直接写出图2中所有的全等三角形(除△ABE≌△ACD外).
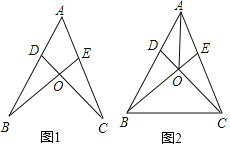
【答案】(1)见解析;(2)△BDC≌△CEB,△DOB≌△EOC,△AOB≌△AOC,△ADO≌△AEO
【解析】
(1)根据“AAS”证明△ABE≌△ACD,从而得到AB=AC;
(2)根据全等三角形的判定方法可得到4对全等三角形.
(1)证明:在△ABE和△ACD 中
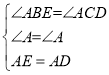 ,
,
∴△ABE≌△ACD (AAS),
∴AB=AC;
(2)解:∵AD=AE,
∴BD=CE,
而△ABE≌△ACD,
∴CD=BE,
∵BD=CE,CD=BE,BC=CB,
∴△BDC≌△CEB(SSS);
∴∠BCD=∠EBC,
∴OB=OC,
∴OD=OE,
而∠BOD=∠COE,
∴△DOB≌△EOC(SAS);
∵AB=AC,∠ABO=∠ACO,BO=CO,
∴△AOB≌△AOC(SAS);
∵AD=AE,OD=OE,AO=AO,
∴△ADO≌△AEO(SSS).


科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
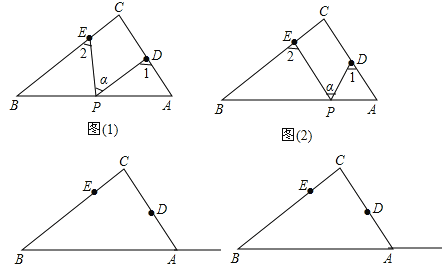
(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2= °;
(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间有何关系?说明理由.
(3)若点P在Rt△ABC斜边BA的延长线上运动(CE<CD),则∠α、∠1、∠2之间有何关系?猜想并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P的坐标是(a,b),从-2,-1,0,1,2这五个数中任取一个数作为a的值,再从余下的四个数中任取一个数作为b的值,则点P(a,b)在平面直角坐标系中第二象限内的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大长方形是由四个小长方形拼成的,请根据此图填空:x2+(p+q)x+pq=x2+px+qx+pq=( )( ).
说理验证
事实上,我们也可以用如下方法进行变形:
x2+(p+q)x+pq=x2+px+qx+pq=(x2+px)+()= =( )( ).
于是,我们可以利用上面的方法进行多项式的因式分解.
尝试运用
例题 把x2+3x+2分解因式.
解:x2+3x+2=x2+(2+1)x+2×1=(x+2)(x+1).
请利用上述方法将下列多项式分解因式:
(1)x2﹣7x+12; (2)(y2+y)2+7(y2+y)﹣18.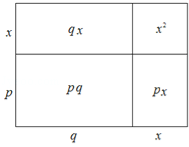
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.

(1)求BD的长;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知边长为2的正三角形ABC顶点A的坐标为(0,6),BC的中点D在y轴上,且在点A下方,点E是边长为2、中心在原点的正六边形的一个顶点,把这个正六边形绕中心旋转一周,在此过程中DE的最小值为( )
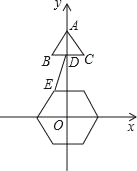
A. 3 B. 4﹣![]() C. 4 D. 6﹣2
C. 4 D. 6﹣2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
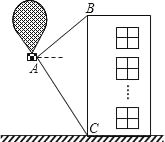
【题目】如图,有一热气球到达离地面高度为36米的A处时,仪器显示正前方一高楼顶部B的仰角是37°,底部C的俯角是60°.为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)(参考数据:参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于点Q。
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,P从点A出发,以1cm/秒的速度向点D运动(不与点D重合),设点P运动时间为t秒,请用t表示PD的长;并求当t为何值时,四边形PBQD是菱形。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com