练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

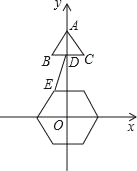
    【题目】如图，已知边长为2的正三角形ABC顶点A的坐标为（0，6），BC的中点D在y轴上，且在点A下方，点E是边长为2、中心在原点的正六边形的一个顶点，把这个正六边形绕中心旋转一周，在此过程中DE的最小值为（　　）

    A. 3 B. 4﹣ C. 4 D. 6﹣2

    【答案】B

    【解析】

    首先得到当点E旋转至y轴上时DE最小，然后分别求得AD、OE′的长，最后求得DE′的长即可．

    如图，当点E旋转至y轴上时DE最小；

    ∵△ABC是等边三角形，D为BC的中点，

    ∴AD⊥BC

    ∵AB=BC=2

    ∴AD=ABsin∠B=，

    ∵正六边形的边长等于其半径，正六边形的边长为2，

    ∴OE=OE′=2

    ∵点A的坐标为（0，6）

    ∴OA=6

    ∴DE′=OA-AD-OE′=4-

    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图所示，MP和NQ分别垂直平分AB和AC.

    (1)若△APQ的周长为12，求BC的长；

    (2)∠BAC＝105°，求∠PAQ的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

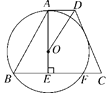
    【题目】如图，梯形ABCD中，AD∥BC，AE⊥BC于点E，∠ADC的平分线交AE于点O，以点O为圆心，OA为半径的圆经过点B，交BC于另一点F.

    (1)求证：CD与⊙O相切；

    (2)若BF＝24，OE＝5，求tan∠ABC的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

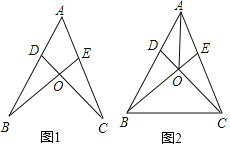
    【题目】如图，AE＝AD，∠ABE＝∠ACD，BE与CD相交于O．

    （1）如图1，求证：AB＝AC；

    （2）如图2，连接BC、AO，请直接写出图2中所有的全等三角形（除△ABE≌△ACD外）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

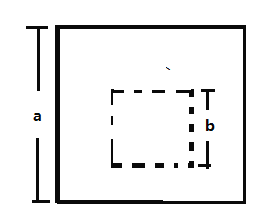
    【题目】数学兴趣小组在“用面积验证平方差公式”时，经历了如下的探究过程；

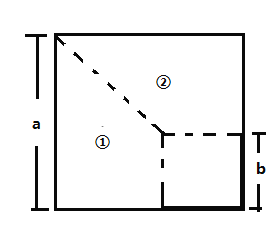
    （1）小明的想法是：将边长为的正方形右下角剪掉一个边长为的正方形(如图1)，将剩下部分按照虚线分割成①和②两部分，并用两种方式表示这两部分面积的和，请你按照小明的想法验证平方差公式．

    （2）小白的想法是：在边长为的正方形内部任意位置剪掉一个边长为的正方形(如图2)，再将剩下部分进行适当分割，并将分割得到的几部分面积和用两种方式表示出来，请你按照小白的想法在图中用虚线画出分割线，并验证平方差公式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某天我国一艘海监船巡航到A港口正西方的B处时，发现在B的北偏东60°方向，相距150海里处的C点有一可疑船只正沿CA方向行驶，C点在A港口的北偏东30°方向上，海监船向A港口发出指令，执法船立即从A港口沿AC方向驶出，在D处成功拦截可疑船只，此时D点与B点的距离为75海里．

    (1)求B点到直线CA的距离；

    (2)执法船从A到D航行了多少海里？（≈1.414，≈1.732，结果精确到0.1海里）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

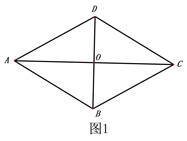
    【题目】如图1，菱形ABCD，AB=4，∠ADC=120o，连接对角线AC、BD交于点O，

    （1）如图2，将△AOD沿DB平移，使点D与点O重合，求平移后的△A′BO与菱形ABCD重合部分的面积.

    （2）如图3，将△A′BO绕点O逆时针旋转交AB于点E′，交BC于点F，

    ①求证：BE′+BF=2，

    ②求出四边形OE′BF的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，已知，，是坐标平面上三点．

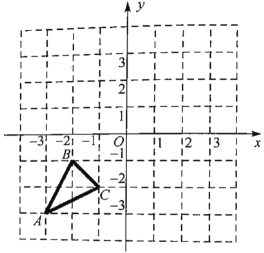
    （1）请画出关于原点对称的．

    （2）请写出点关于轴对称的点的坐标，若将点向上平移个单位，使其落在内部，指出的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD内接于⊙O，点P是上一点，连接PB、PC，若AD=2AB，则cos∠BPC的值为（　　）

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案