
【题目】如图,大长方形是由四个小长方形拼成的,请根据此图填空:x2+(p+q)x+pq=x2+px+qx+pq=( )( ).
说理验证
事实上,我们也可以用如下方法进行变形:
x2+(p+q)x+pq=x2+px+qx+pq=(x2+px)+()= =( )( ).
于是,我们可以利用上面的方法进行多项式的因式分解.
尝试运用
例题 把x2+3x+2分解因式.
解:x2+3x+2=x2+(2+1)x+2×1=(x+2)(x+1).
请利用上述方法将下列多项式分解因式:
(1)x2﹣7x+12; (2)(y2+y)2+7(y2+y)﹣18.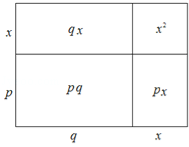
【答案】x+p x+q qx+pq x(x+p)+q(x+p) x+p x+q
(1)(x﹣3)(x﹣4) (2)(y2+y+9)(y+2)(y﹣1)
【解析】
试题由矩形的面积公式可以求得x2+px+qx+pq=(x+p)(x+q);
利用分组的方法可以先分组然后提公因式法可以分解因式为:x2+px+qx+pq=(x2+px)+(qx+pq)=x(x+p)+q(x+p)=(x+p)(x+q);
根据x2+(p+q)x+pq=(x+p)(x+q)的形式的运用,可以将一个二次三项式分解因式,从而求出结果.
解:由矩形的面积公式得:(x+p)(x+q);
根据分组分解法得:x(x+p)+q(x+p),(x+p)(x+q);
(1)原式=(x﹣3)(x﹣4)
(2)原式=(y2+y+9)(y2+y﹣2)
=(y2+y+9)(y+2)(y﹣1).
故答案为(x+p)(x+q);x(x+p)+q(x+p),(x+p)(x+q);


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已如点A(1,1),B(-1,1),C(-1,-2),D(1,-2),把一根长为2019个单位长度没有弹性的细线(线的相细忽略不计)的一端固定在A处,并按![]() 的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是__________.
的规律紧绕在四边形ABCD的边上,则细线的另一端所在位置的点的坐标是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个有进水管与出水管的容器,从某时刻开始![]() 分钟内只进水不出水.在随后的
分钟内只进水不出水.在随后的![]() 分钟内既进水又出水,直到容器内的水量达到
分钟内既进水又出水,直到容器内的水量达到![]() .如图,坐标系中的折线段
.如图,坐标系中的折线段![]() 表示这一过程中容器内的水量
表示这一过程中容器内的水量![]() (单位:
(单位:![]() )与时间
)与时间![]() (单位:分)之间的关系.
(单位:分)之间的关系.
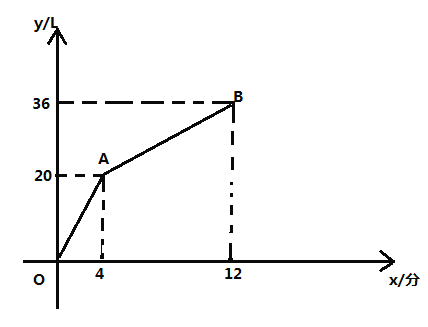
(1)单独开进水管,每分钟可进水________![]() ;
;
(2)求进水管与出水管同时打开时容器内的水量![]() 与时间
与时间![]() 的函数关系式
的函数关系式![]() ;
;
(3)当容器内的水量达到![]() 时,立刻关闭进水管,直至容器内的水全部放完.请在同一坐标系中画出表示放水过程中容器内的水量
时,立刻关闭进水管,直至容器内的水全部放完.请在同一坐标系中画出表示放水过程中容器内的水量![]() 与时间
与时间![]() 关系的线段
关系的线段![]() ,并直接写出点
,并直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
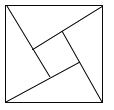
【题目】如图的图形取材于我国古代数学家赵爽的《勾股圆方图》也称(《赵爽弦图》),它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如图所示,如果大正方形的面积是![]() ,小正方形的面积是
,小正方形的面积是![]() ,直角三角形较短的直角边为
,直角三角形较短的直角边为![]() ,较长的直角边为
,较长的直角边为![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
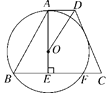
【题目】如图,梯形ABCD中,AD∥BC,AE⊥BC于点E,∠ADC的平分线交AE于点O,以点O为圆心,OA为半径的圆经过点B,交BC于另一点F.
(1)求证:CD与⊙O相切;
(2)若BF=24,OE=5,求tan∠ABC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘船以每小时![]() 海里的速度向西南方向航行,在
海里的速度向西南方向航行,在![]() 处观测灯塔
处观测灯塔![]() 在船的南偏西
在船的南偏西![]() 的方向,航行
的方向,航行![]() 分钟后到达
分钟后到达![]() 处,这时灯塔
处,这时灯塔![]() 恰好在船的正西方向.已知距离此灯塔
恰好在船的正西方向.已知距离此灯塔![]() 海里以内的海区有暗礁,这艘船继续沿西南方向航行是否有触礁的危险?为什么?(参考数据:
海里以内的海区有暗礁,这艘船继续沿西南方向航行是否有触礁的危险?为什么?(参考数据:![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
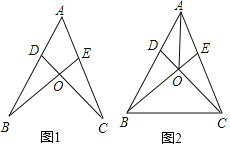
【题目】如图,AE=AD,∠ABE=∠ACD,BE与CD相交于O.
(1)如图1,求证:AB=AC;
(2)如图2,连接BC、AO,请直接写出图2中所有的全等三角形(除△ABE≌△ACD外).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(![]() ≈1.414,
≈1.414,![]() ≈1.732,结果精确到0.1海里)
≈1.732,结果精确到0.1海里)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com