
����Ŀ��һ���н�ˮ�����ˮ�ܵ���������ijʱ�̿�ʼ![]() ������ֻ��ˮ����ˮ��������
������ֻ��ˮ����ˮ��������![]() �����ڼȽ�ˮ�ֳ�ˮ��ֱ�������ڵ�ˮ���ﵽ
�����ڼȽ�ˮ�ֳ�ˮ��ֱ�������ڵ�ˮ���ﵽ![]() ����ͼ������ϵ�е����߶�
����ͼ������ϵ�е����߶�![]() ��ʾ��һ�����������ڵ�ˮ��
��ʾ��һ�����������ڵ�ˮ��![]() ����λ��
����λ��![]() ����ʱ��
����ʱ��![]() ����λ���֣�֮��Ĺ�ϵ��
����λ���֣�֮��Ĺ�ϵ��
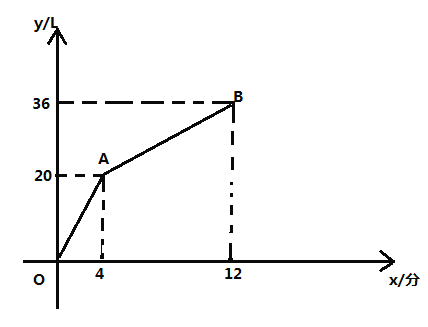
��1����������ˮ�ܣ�ÿ���ӿɽ�ˮ________![]() ��
��
��2�����ˮ�����ˮ��ͬʱ��ʱ�����ڵ�ˮ��![]() ��ʱ��
��ʱ��![]() �ĺ�����ϵʽ
�ĺ�����ϵʽ![]() ��
��
��3���������ڵ�ˮ���ﵽ![]() ʱ�����̹رս�ˮ�ܣ�ֱ�������ڵ�ˮȫ�����꣮����ͬһ����ϵ�л�����ʾ��ˮ�����������ڵ�ˮ��
ʱ�����̹رս�ˮ�ܣ�ֱ�������ڵ�ˮȫ�����꣮����ͬһ����ϵ�л�����ʾ��ˮ�����������ڵ�ˮ��![]() ��ʱ��
��ʱ��![]() ��ϵ���߶�
��ϵ���߶�![]() ����ֱ��д����
����ֱ��д����![]() �����꣮
�����꣮
���𰸡���1��![]() ����2��
����2��![]()
![]() ����3����
����3����![]() ������Ϊ
������Ϊ![]() ��
��
��������
��1������4����ˮ���ﵽ![]() ������⣻
������⣻
��2����![]() ��
��![]() ֮��ĺ�����ϵʽΪ
֮��ĺ�����ϵʽΪ![]()
![]() �����ô���ϵ����������⣻
�����ô���ϵ����������⣻
��3�������ˮ��ÿ���ӵij�ˮ��������������ڵ�ˮȫ�������ʱ�䣬�õ�C�����꼴����ͼ��
��1����������ˮ�ܣ�ÿ���ӿɽ�ˮ20��4=![]()
![]()
�ʴ�Ϊ��5��
��2����![]() ��
��![]() ֮��ĺ�����ϵʽΪ
֮��ĺ�����ϵʽΪ![]() ��
��
��![]() ��
��![]() ����
����![]() ��
�У�
��![]()
�⣬��![]() ��
��
���ԣ�![]() ��
��![]() ֮��ĺ�����ϵʽΪ
֮��ĺ�����ϵʽΪ![]()
![]() ��
��
��3�����ˮ��ÿ���ӵij�ˮ��Ϊa��
����ɵã�12-4������5-a��=36-20
���a=3
�������ڵ�ˮȫ�������ʱ��Ϊ36��3=12�����ӣ�
��C![]()
��ͼ���߶�![]() ��Ϊ����
������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
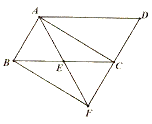
����Ŀ����ͼ����E��ƽ���ı���ABCD�ı�BC���е㣬����AE���ӳ���DC���ӳ����ڵ�F,����AC��BF,��AEC=2��ABC��(1)��֤:�ı���ABFC�Ǿ��Σ�(2)��(1)��������,����AFD�ǵȱ�������,�ұ߳�Ϊ4,���ı���ABFC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Rt��ABC�У���C=90�㣬��D��E�ֱ��ǡ�ABC��AC��BC�ϵĵ㣬��P��һ���㣮���PDA=��1����PEB=��2����DPE=�Ϧ���
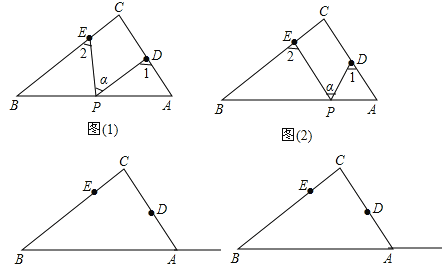
��1������P���߶�AB�ϣ���ͼ��1����ʾ���ҡϦ�=50�㣬���1+��2= �㣻
��2������P�ڱ�AB���˶�����ͼ��2����ʾ����Ϧ�����1����2֮���кι�ϵ��˵��������
��3������P��Rt��ABCб��BA���ӳ������˶���CE��CD������Ϧ�����1����2֮���кι�ϵ�����벢˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
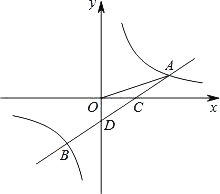
����Ŀ����ͼ��һ�κ���y=ax��1��ͼ���뷴��������y=![]() ��ͼ����A��B���㣬��x�ύ�ڵ�C����y�ύ�ڵ�D����֪OA=
��ͼ����A��B���㣬��x�ύ�ڵ�C����y�ύ�ڵ�D����֪OA=![]() ��tan��AOC=
��tan��AOC=![]() ��
��
��1����a��k��ֵ����B�����ꣻ
��2���۲�ͼ����ֱ��д������ʽax��1��![]() �Ľ⼯��
�Ľ⼯��
��3����y���ϴ���һ��P��ʹ����PDC����ODC���ƣ��������P������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ۺ���ʵ����ѧϰ�������һ�������Σ�����Щ�����ε����߷ֱ�Ϊ![]() ��
��![]() ��
��![]() ���üǺ�
���üǺ�![]() ��ʾһ�����������������Σ���
��ʾһ�����������������Σ���![]() ��ʾ�߳��ֱ�Ϊ2��4��4����λ���ȵ�һ�������Σ�
��ʾ�߳��ֱ�Ϊ2��4��4����λ���ȵ�һ�������Σ�
��1������Щ���������ߵij���Ϊ����0��С��3����������λ���ȣ����üǺ�д���������������������Σ�
��2����ͼ��![]() ��
��![]() �����ߣ��߶�
�����ߣ��߶�![]() ��
��![]() �ij��ȷֱ�Ϊ2����6����λ���ȣ����߶�
�ij��ȷֱ�Ϊ2����6����λ���ȣ����߶�![]() �ij���Ϊ��������λ���ȣ�����
�ij���Ϊ��������λ���ȣ�����![]() ��
��![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]()
����![]() ֮����
֮����
����ֱ���üǺű�ʾ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
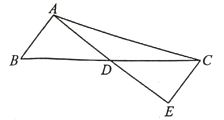
����Ŀ����ͼ�������������У�����֤����ABD�ա�ACD���ǣ� ��.

A.BD=DC�� AB=AC B.��ADB=��ADC��BD=DC
C.��B=��C����BAD=��CAD D. ��B=��C��BD=DC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P����������a,b������-2��-1,0,1,2�����������ȡһ������Ϊa��ֵ���ٴ����µ��ĸ�������ȡһ������Ϊb��ֵ�����P��a,b����ƽ��ֱ������ϵ�еڶ������ڵĸ����� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����������ĸ�С������ƴ�ɵģ�����ݴ�ͼ��գ�x2+��p+q��x+pq=x2+px+qx+pq=������������������
˵����֤
��ʵ�ϣ�����Ҳ���������·������б��Σ�
x2+��p+q��x+pq=x2+px+qx+pq=��x2+px��+����=����=������������������
���ǣ����ǿ�����������ķ������ж���ʽ����ʽ�ֽ⣮
��������
���� ��x2+3x+2�ֽ���ʽ��
�⣺x2+3x+2=x2+��2+1��x+2��1=��x+2����x+1����
�������������������ж���ʽ�ֽ���ʽ��
��1��x2��7x+12�� ��2����y2+y��2+7��y2+y����18��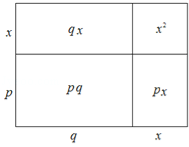
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
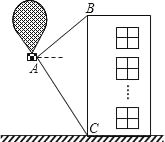
����Ŀ����ͼ����һ�����������߶�Ϊ36��A��ʱ��������ʾ��ǰ��һ��¥����B��������37�����ײ�C�ĸ�����60����Ϊ�˰�ȫ��Խ��¥������Ӧ���������������ף��������ȷ��0.1�ף����ο����ݣ��ο����ݣ�sin37���0.60��cos37���0.80��tan37���0.75��![]() ��1.73��
��1.73��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com