练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图所示，△ABC的三个顶点的坐标分别为A（﹣1，3）、B（﹣2，﹣2）、C（4，﹣2），则△ABC外接圆半径的长度为_____．

    【答案】

    【解析】

    根据三角形的外心是三边中垂线的交点，由B、C的坐标可知，圆心M必在直线x=1上；由图知：AC的垂直平分线正好经过（1，0），由此可得到M（1，0）；连接MB，过M作MD⊥BC于D，由勾股定理即可求得 M的半径长．

    设△ABC的外心为M;

    ∵B(2,2),C(4,2)，

    ∴M必在直线x=1上，

    由图知：AC的垂直平分线过(1,0)，

    故M(1,0)；

    过M作MD⊥BC于D，连接MB，

    Rt△MBD中，MD=2，BD=3，

    由勾股定理得：MB==，

    即△ABC的外接圆半径为.

    故答案为：.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形ABCD中，P是BC的中点，把△PAB沿着PA翻折得到△PAE，过C作CF⊥DE于F，若CF=2，则DF=_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

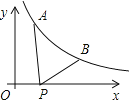
    【题目】如图所示，已知A（，y1），B(2,y2)为反比例函数图像上的两点，动点P(x，0)在x正半轴上运动，当线段AP与线段BP之差达到最大时，点P的坐标是（ ）

    A. (，0) B. (1,0) C. (,0) D. (,0)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

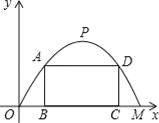
    【题目】施工队要修建一个横断面为抛物线的公路隧道，其高度为6米，宽度OM为12米，现在O点为原点，OM所在直线为x轴建立直角坐标系（如图所示）．

    （1）直接写出点M及抛物线顶点P的坐标；

    （2）求出这条抛物线的函数解析式；

    （3）施工队计划在隧道门口搭建一个矩形“脚手架”ABCD，使A、D点在抛物线上，B、C点在地面OM上．为了筹备材料，需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少？请你帮施工队计算一下．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】利用“同角的余角相等”可以帮助我们得到相等的角，这个规律在全等三角形的判定中有着广泛的运用．

    （1）如图①，，，三点共线，于点，于点，，且．若，求的长．

    （2）如图②，在平面直角坐标系中，为等腰直角三角形，直角顶点的坐标为，点的坐标为．求直线与轴的交点坐标．

    （3）如图③，，平分，若点坐标为，点坐标为．则 ．（只需写出结果，用含，的式子表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

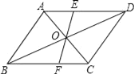
    【题目】如图，过平行四边形ABCD对角线交点O的直线交AD于E，交BC于F，若AB=5，BC=6，OE=2，那么四边形EFCD周长是（　　）

    A. 16B. 15C. 14D. 13

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，E、F、 G、H分别为四边形ABCD四边之中点．

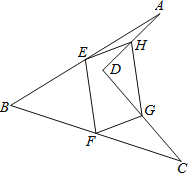
    (1)求证：四边形EFGH为平行四边形；

    (2)当AC、BD满足______时，四边形EFGH为矩形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

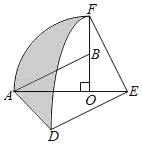
    【题目】如图，在Rt△AOB中，∠AOB=90°，OA=2，OB=1，将Rt△AOB绕点O顺时针旋转90°后得到Rt△FOE，将线段EF绕点E逆时针旋转90°后得到线段ED，分別以O、E为圆心，OA、ED长为半径画弧AF和弧DF，连接AD，则图中阴影部分的面积是__．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）问题发现

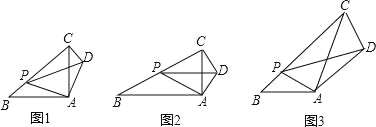
    如图1，在Rt△ABC中，∠A=90°，=1，点P是边BC上一动点（不与点B重合），∠PAD=90°，∠APD=∠B，连接 CD．

    （1）①求的值；②求∠ACD的度数．

    （2）拓展探究

    如图 2，在Rt△ABC中，∠A=90°，=k．点P是边BC上一动点（不与点B重合），∠PAD=90°，∠APD=∠B，连接CD，请判断∠ACD与∠B 的数量关系以及PB与CD之间的数量关系，并说明理由．

    （3）解决问题

    如图 3，在△ABC中，∠B=45°，AB=4，BC=12，P 是边BC上一动点（不与点B重合），∠PAD=∠BAC，∠APD=∠B，连接CD．若 PA=5，请直接写出CD的长．

    查看答案和解析>>

    同步练习册答案