
【题目】如图,E、F、 G、H分别为四边形ABCD四边之中点.
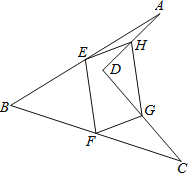
(1)求证:四边形EFGH为平行四边形;
(2)当AC、BD满足______时,四边形EFGH为矩形.
【答案】(1)见解析;(2)AC⊥BD
【解析】
(1)连接BD,根据中位线的性质可得EH∥BD,EH=![]() ,FG∥BD,FG=
,FG∥BD,FG=![]() ,从而得出EH∥FG,EH= FG,然后根据平行四边形的判定定理即可证出结论;
,从而得出EH∥FG,EH= FG,然后根据平行四边形的判定定理即可证出结论;
(2)当AC⊥BD时,连接AC,根据中位线的性质可得EF∥AC,从而得出EF⊥BD,然后由(1)的结论可证出EF⊥EH,最后根据有一个角是直角的平行四边形是矩形即可证出结论.
(1)证明:连接BD
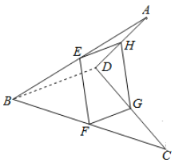
∵E、F、 G、H分别为四边形ABCD四边的中点
∴EH是△ABD的中位线,FG是△CBD的中位线
∴EH∥BD,EH=![]() ,FG∥BD,FG=
,FG∥BD,FG=![]()
∴EH∥FG,EH= FG
∴四边形EFGH为平行四边形;
(2)当AC⊥BD时,四边形EFGH为矩形,理由如下
连接AC,
∵E、F为BA和BC的中点
∴EF为△BAC的中位线
∴EF∥AC
∵AC⊥BD
∴EF⊥BD
∵EH∥BD
∴EF⊥EH
∴∠FEH=90°
∵四边形EFGH为平行四边形
∴四边形EFGH为矩形
故答案为:AC⊥BD.


科目:初中数学 来源: 题型:
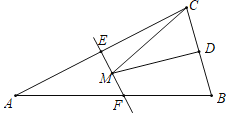
【题目】如图,等腰三角形ABC的底边BC长为6,面积是18,腰AC的垂直平分线EF分别交AC,AB于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则△CDM的周长的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
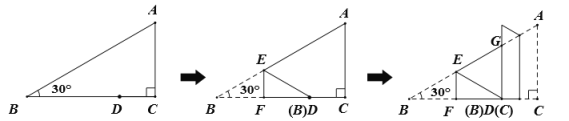
【题目】在三角形纸片![]() 中,
中,![]() ,
,![]() ,点
,点![]() (不与
(不与![]() ,
,![]() 重合)是
重合)是![]() 上任意一点,将此三角形纸片按下列方式折叠,若
上任意一点,将此三角形纸片按下列方式折叠,若![]() 的长度为
的长度为![]() ,则
,则![]() 的周长为__________.(用含
的周长为__________.(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为解决部分市民冬季集中取暖问题,需铺设一条长4000米的管道,为尽量减少施工对交通造成的影响,施工时“…”,设实际每天铺设管道x米,则可得方程![]() =20,根据此情景,题中用“…”表示的缺失的条件应补为( )
=20,根据此情景,题中用“…”表示的缺失的条件应补为( )
A. 每天比原计划多铺设10米,结果延期20天完成
B. 每天比原计划少铺设10米,结果延期20天完成
C. 每天比原计划多铺设10米,结果提前20天完成
D. 每天比原计划少铺设10米,结果提前20天完成
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有两辆玩具车进行30米的直跑道比赛,两车从起点同时出发,A车到达终点时,B车离终点还差12米,A车的平均速度为2.5米/秒.
(1)求B车的平均速度;
(2)如果两车重新比赛,A车从起点退后12米,两车能否同时到达终点?请说明理由;
(3)在(2)的条件下,若调整A车的平均速度,使两车恰好同时到达终点,求调整后A车的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
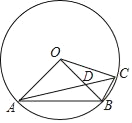
【题目】如图,⊙O是△ABC的外接圆,OA=2cm,OA⊥OB,AC交OB于D点,AD=2CD.
(1)求∠BOC的度数;
(2)求线段BD、线段CD和 BC围成的图形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com