
【题目】已知有两辆玩具车进行30米的直跑道比赛,两车从起点同时出发,A车到达终点时,B车离终点还差12米,A车的平均速度为2.5米/秒.
(1)求B车的平均速度;
(2)如果两车重新比赛,A车从起点退后12米,两车能否同时到达终点?请说明理由;
(3)在(2)的条件下,若调整A车的平均速度,使两车恰好同时到达终点,求调整后A车的平均速度.
【答案】(1) B车的平均速度为![]() 米/秒;(2)不能,理由见解析;(3) A车调整后的平均速度为
米/秒;(2)不能,理由见解析;(3) A车调整后的平均速度为![]() 米/秒
米/秒
【解析】
(1) A车走完全程所用时间![]() 秒就是B车走了路程(30-12)米所花的时间,据此列出方程并解得即可;
秒就是B车走了路程(30-12)米所花的时间,据此列出方程并解得即可;
(2)比较A车走完全程(30+12)与B车走了路程所花的时间,即可得到答案;
(3)由(2)的结论:B车到达终点所花时间为![]() 秒,即可求得A车调整后的平均速度.
秒,即可求得A车调整后的平均速度.
(1)设B车的平均速度为![]() 米/秒,
米/秒,
依题意得:![]()
解得:![]()
∴B车的平均速度为![]() 米/秒;
米/秒;
(2)不能,理由是:
A车从起点退后12米,再到达终点所花时间为:![]() 秒;
秒;
B车到达终点所花时间为:![]() 秒;
秒;
∴A车比B车先到达终点;
(3)由(2)的结论:B车到达终点所花时间为![]() 秒;
秒;
∴A车调整后的平均速度应为:![]() 米/秒.
米/秒.


科目:初中数学 来源: 题型:
【题目】下图反映了初三(1)班、(2)班的体育成绩。

(1)不用计算,根据条形统计图,_______班学生的体育成绩好一些。
(2)从图中观察出:三(1)班学生体育成绩等级的众数是_______;三(2)班学生体育成绩等级的众数是_______.
(3)如果依次将不及格、及格、中、良好、优秀记为55、65、75、85、95分,请你观察计算一下初三(1),(2)班的平均成绩各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 以上均不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为_____.
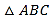
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,BD=CE,将线段AE沿AC翻折,得到线段AM,连结EM交AC于点N,连结DM、CM以下说法:①AD=AM,②∠MCA=60°,③CM=2CN,④MA=DM中,正确的有( )

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一种成本为![]() 元
元![]() 的水产品,若按
的水产品,若按![]() 元
元![]() 销售,一个月可售出
销售,一个月可售出![]() ,售价毎涨
,售价毎涨![]() 元,月销售量就减少
元,月销售量就减少![]() .
.
![]() 写出月销售利润
写出月销售利润![]() (元)与售价
(元)与售价![]() (元
(元![]() )之间的函数表达式;
)之间的函数表达式;
![]() 当售价定为多少元时,该商店月销售利润为
当售价定为多少元时,该商店月销售利润为![]() 元?
元?
![]() 当售价定为多少元时会获得最大利润?求出最大利润.
当售价定为多少元时会获得最大利润?求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABO放在平面直角坐标系中,点A、B分别在y轴、x轴上,∠BAO=30°,BC是∠ABO的角平分线,交y轴于点C(0,﹣2),CD⊥AB,垂足为D

(1)求BC的长度.
(2)点P(0,n)是线段AO上的任意一点(点P不与A、C、O重合),以BP为边,在BD的下方画出∠BPE=60°,PE交CD的延长线于点E,在备用图中画出图形,并求CE的长(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作:如图,在已知内角度数的三个三角形中,请用直尺从某一顶点画一条线段,把原三角形分割成两个等腰三角形,并在图中标注相应的角的度数
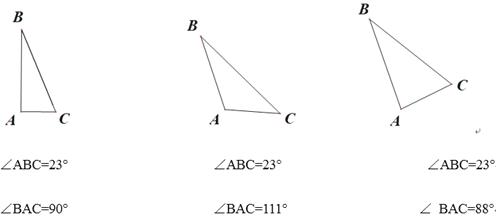
(2)拓展,△ABC中,AB=AC,∠A=45°,请把△ABC分割成三个等腰三角形,并在图中标注相应的角的度数.
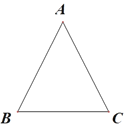
(3)思考在如图所示的三角形中∠A=30°.点P和点Q分别是边AC和BC上的两个动点.分别连接BP和PQ把△ABC分割成三个三角形.△ABP,△BPQ,△PQC若分割成的这三个三角形都是等腰三角形,求∠C的度数所有可能值直接写出答案即可.
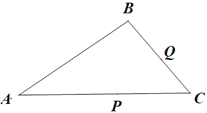
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com