
【题目】(1)操作:如图,在已知内角度数的三个三角形中,请用直尺从某一顶点画一条线段,把原三角形分割成两个等腰三角形,并在图中标注相应的角的度数
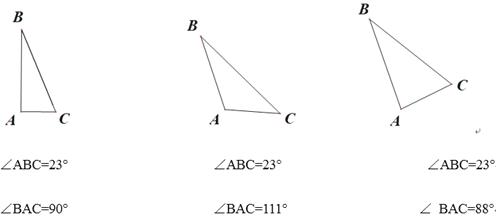
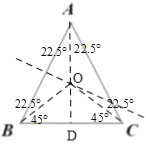
(2)拓展,△ABC中,AB=AC,∠A=45°,请把△ABC分割成三个等腰三角形,并在图中标注相应的角的度数.
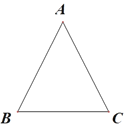
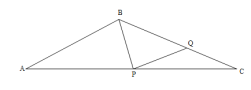
(3)思考在如图所示的三角形中∠A=30°.点P和点Q分别是边AC和BC上的两个动点.分别连接BP和PQ把△ABC分割成三个三角形.△ABP,△BPQ,△PQC若分割成的这三个三角形都是等腰三角形,求∠C的度数所有可能值直接写出答案即可.
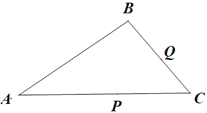
【答案】(1)见解析;(2)见解析;(3)∠C所有可能的值为10°、20°、25°,35°、40°、50°、80°、100°.
【解析】
(1)在图1、图2、图3中,分别作AB、AB、BC的垂直平分线,根据垂直平分线的性质及外角的性质求出各角度数即可;(2)分别作AB、BC的垂直平分线,交于点O,连接OA、OB、OC可得三角形OAB、OAC、OBC为等腰三角形,根据等腰三角形的性质及外角性质求出各角度数即可;(3)分PB=PA、AB=AP、BA=BP时,PB=PQ、BP=BQ、QB=QP,PQ=QC、PC=QC、PQ=PC等10种情况,根据等腰三角形的性质分别求出∠C的度数即可.
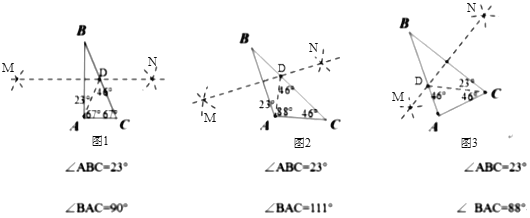
(1)在图1、图2、图3中,分别作AB、AB、BC的垂直平分线,
如图1,∵∠ABC=23°,∠BAC=90°,
∴∠C=90°-23°=67°,
∵MN垂直平分AB,
∴BD=AD,
∴△ABD是等腰三角形,
∴∠BAD=∠ABC=23°,
∴∠ADC=2∠ABC=46°,
∵∠BAC=90°,
∴∠DAC=∠BAC-∠BAD=67°,
∴∠DAC=∠C,
∴△DAC是等腰三角形,
同理:图2中,∠ADC=46°,∠DAC=88°,∠C=46°,△ABD和△ACD是等腰三角形,
图3中,∠BCD=23°,∠ADC=46°,∠ACD=46°,△BCD和△ACD是等腰三角形.
(2)作AB、BC的垂直平分线,交于点O,连接OA、OB、OC,
∵点O是三角形垂直平分线的交点,
∴OA=OB=OC,
∴△OAB、△OAC、△OBC是等腰三角形,
∵AB=AC,∠BAC=45°,
∴∠ABC=∠ACB=67.5°,
∴AD是BC的垂直平分线,
∴∠BAD=∠CAD=22.5°,
∴∠OBA=∠OAB=22.5°,∠OCA=∠OAC=22.5°,
∴∠OBC=∠OCB=45°.
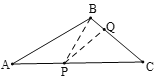
(3)①如图,当PB=PA,PB=PQ,PQ=CQ时,
∵∠A=30°,PB=PQ,
∴∠ABP=∠A=30°,
∴∠APB=120°,
∵PB=PQ,PQ=CQ,
∴∠PQB=∠PBQ,∠C=∠CPQ,
∴∠PBQ=2∠C,
∴∠APB=∠PBQ+∠C=3∠C=120°,
解得:∠C=40°.
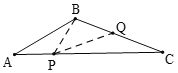
②如图,当PB=PA,PB=BQ,PQ=CQ时,
∴∠PQB=2∠C,∠PQB=∠BPQ,
∴∠PBQ=180°-2∠PQB=180°-4∠C,
∴180°-4∠C+∠C=120°,
解得:∠C=20°,
③如图,当PA=PB,BQ=PQ,CQ=CP时,
∵∠PQC=2∠PBQ,∠PQC=![]() (180°-∠C),
(180°-∠C),
∴∠PBQ=![]() (180°-∠C),
(180°-∠C),
∴![]() (180°-∠C)+∠C=120°,
(180°-∠C)+∠C=120°,
解得:∠C=100°.
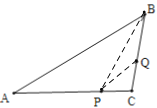
④如图,当PA=PB,BQ=PQ,PQ=CP时,
∵∠PQC=∠C=2∠PBQ,
又∵∠C+∠PBQ=120°,
∴∠C=80°;
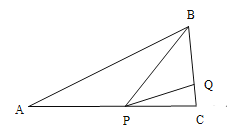
⑤如图,当AB=AP,BP=BQ,PQ=QC时,
∵∠A=30°,
∴∠APB=![]() (180°-30°)=75°,
(180°-30°)=75°,
∵BP=BQ,PQ=CQ,
∴∠BPQ=∠BQP,∠QPC=∠QCP,
∴∠BQP=2∠C,
∴∠PBQ=180°-4∠C,
∴∠C+180°-4∠C=75°,
解得:∠C=35°.
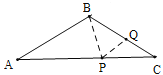
⑥如图,当AB=AP,BQ=PQ,PC=QC时,
∴∠PQC=2∠PBC,∠PQC=![]() (180°-∠C),
(180°-∠C),
∴∠PBC=![]() (180°-∠C),
(180°-∠C),
∴![]() (180°-∠C)+∠C=75°,
(180°-∠C)+∠C=75°,
解得:∠C=40°.
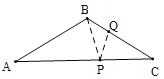
⑦如图,当AB=AP,BQ=PQ,PC=QP时,
∵∠C=∠PQC=2∠PBC,∠C+∠PQC=75°,
∴∠C=50°;
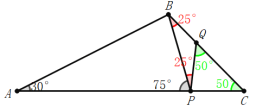
⑧当AB=AP,BP=PQ,PQ=CQ时,
∵AB=BP,∠A=30°,
∴∠ABP=∠APB=75°,
又∵∠PBQ=∠PQB=2∠C,
且有∠PBQ+∠C=180°-30°-75°=75°,
∴3∠C=75°,
∴∠C=25°;
⑨当AB=BP,BP=PQ,PQ=CQ时,
∵AB=BP,
∴∠BPA=∠A=30°,
∵∠PBQ=∠PQB=2∠C,
∴2∠C+∠C=30°,
解得:∠C=10°.

⑩当AB=BP,BQ=PQ,PQ=CQ时,
∴∠PQC=∠C=2∠PBQ,
∴![]() ∠C+∠C=30°,
∠C+∠C=30°,
解得:∠C=20°.
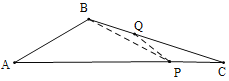
综上所述:∠C所有可能的值为10°、20°、25°,35°、40°、50°、80°、100°.


科目:初中数学 来源: 题型:
【题目】已知有两辆玩具车进行30米的直跑道比赛,两车从起点同时出发,A车到达终点时,B车离终点还差12米,A车的平均速度为2.5米/秒.
(1)求B车的平均速度;
(2)如果两车重新比赛,A车从起点退后12米,两车能否同时到达终点?请说明理由;
(3)在(2)的条件下,若调整A车的平均速度,使两车恰好同时到达终点,求调整后A车的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形MNPQ中,动点R从点N出发,沿着N-P-Q-M方向移动至M停止,设R移动路程为x,MNR面积为y,那么y与x的关系如图②,下列说法不正确的是( )

A.当x=2时,y=5B.矩形MNPQ周长是18
C.当x=6时,y=10D.当y=8时,x=10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】浠水县商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A![]() B
B![]() C
C![]() ;
;
(2) 请画出△ABC关于原点对称的△A![]() B
B![]() C
C![]() ;
;
(3) 在![]() 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直于直线CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图2),找出图中与BE相等的线段,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,斜边AB的垂直平分线交AB于点D,交BC于点E,AE平分∠BAC,那么下列不成立的是( )

A.∠B=∠CAEB.∠DEA=∠CEAC.∠B=∠BAED.AC=2EC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠C=90°,延长CA至点D,使AD=AB.设F为线段AB上一点,连接DF,以DF为斜边作等腰Rt△DEF,且使AE⊥AB.
(1)求证:AE=AF+BC;
(2)当点F为BA延长线上一点,而其余条件保持不变,如图2所示,试探究AE、AF、BC之间的数量关系,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com