Question

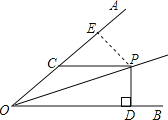
【题目】如图，∠AOB=30°，OP平分∠AOB，PD⊥OB于D，PC∥OB交OA于C，若PC=6，则PD= ．

Answer 1

【答案】3．

【解析】

试题分析：过点P作PE⊥OA于E，根据角平分线定义可得∠AOP=∠BOP=15°，再由两直线平行，内错角相等可得∠BOP=∠OPC=15°，然后利用三角形的一个外角等于与它不相邻的两个内角的和求出∠PCE=30°，再根据直角三角形30°角所对的直角边等于斜边的一半解答．

解：如图，过点P作PE⊥OA于E，

∵∠AOB=30°，OP平分∠AOB，

∴∠AOP=∠BOP=15°．

∵PC∥OB，

∴∠BOP=∠OPC=15°，

∴∠PCE=∠AOP+∠OPC=15°+15°=30°，

又∵PC=6，

∴PE=PC=3，

∵∠AOP=∠BOP，PD⊥OB于D，PE⊥OA于E，

∴PD=PE=3，

故答案为3．