
【题目】如图所示,小明家小区空地上有两棵笔直的树![]() 、
、![]() .一天,他在
.一天,他在![]() 处测得树顶
处测得树顶![]() 的仰角
的仰角![]() ,在
,在![]() 处测得树顶
处测得树顶![]() 的仰角
的仰角![]() ,线段
,线段![]() 恰好经过树顶
恰好经过树顶![]() .已知.
.已知. ![]() 、
、![]() 两处的距离为
两处的距离为![]() 米,两棵树之间的距离
米,两棵树之间的距离![]() 米,
米, ![]() 、
、![]() 、
、![]() 、
、![]() 四点在一条直线上,求树
四点在一条直线上,求树![]() 的高度.(
的高度.(![]() ,
, ![]() ,结果精确到
,结果精确到![]() )
)

【答案】树EF的高度约为5.7m.
【解析】试题分析:设CD=xm,先在Rt△BCD中,由于∠DBC=45°,则根据等腰直角三角形的性质得BC=CD=x,再在Rt△DAC中,利用正切定义得到x+2=![]() x,解得x=
x,解得x=![]() +1,即BC=CD=
+1,即BC=CD=![]() +1,然后在Rt△FBE中根据等腰直角三角形的性质得FE=BE=BC+CE≈5.7.
+1,然后在Rt△FBE中根据等腰直角三角形的性质得FE=BE=BC+CE≈5.7.
试题解析:解:设CD=xm,在Rt△BCD中,∵∠DBC=45°,∴BC=CD=x,在Rt△DAC中,∵∠DAC=30°,∴tan∠DAC=![]() ,∴x+2=
,∴x+2=![]() x,解得x=
x,解得x=![]() +1,∴BC=CD=
+1,∴BC=CD=![]() +1,在Rt△FBE中,∵∠DBC=45°,∴FE=BE=BC+CE=
+1,在Rt△FBE中,∵∠DBC=45°,∴FE=BE=BC+CE=![]() +1+3≈5.7.
+1+3≈5.7.
答:树EF的高度约为5.7m.


科目:初中数学 来源: 题型:
【题目】金瑞公司决定从厂家购进甲、乙两种不同型号的显示器共50台,购进显示器的总金额不超过77000元,已知甲、乙型号的显示器价格分别为1000元/台、2000元/台.
(1)求金瑞公司至少购进甲型显示器多少台?
(2)若甲型显示器的台数不超过乙型显示器的台数,则有哪些购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一棵大树在一次强台风中折断倒下,未折断树杆![]() 与地面仍保持垂直的关系,而折断部分
与地面仍保持垂直的关系,而折断部分![]() 与未折断树杆
与未折断树杆![]() 形成
形成![]() 的夹角.树杆
的夹角.树杆![]() 旁有一座与地面垂直的铁塔
旁有一座与地面垂直的铁塔![]() ,测得
,测得![]() 米,塔高
米,塔高![]() 米.在某一时刻的太阳照射下,未折断树杆
米.在某一时刻的太阳照射下,未折断树杆![]() 落在地面的影子
落在地面的影子![]() 长为
长为![]() 米,且点
米,且点![]() 、
、![]() 、
、![]() 、
、![]() 在同一条直线上,点
在同一条直线上,点![]() 、
、![]() 、
、![]() 也在同一条直线上.求这棵大树没有折断前的高度.(结果精确到
也在同一条直线上.求这棵大树没有折断前的高度.(结果精确到![]() ,参考数据:
,参考数据: ![]() ,
, ![]() ,
, ![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个菱形绕着它的对角线的交点旋转![]() ,旋转前后的两个菱形构成一个“星形”(阴影部分).若菱形的一个内角为
,旋转前后的两个菱形构成一个“星形”(阴影部分).若菱形的一个内角为![]() ,边长为
,边长为![]() ,则该“星形”的面积是__________.
,则该“星形”的面积是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请把下列证明过程补充完整(括号内填写相应的理由)
已知:如图,点E在BC延长线上,AE交CD于点F,AD∥BC,∠1=∠2,∠3=
∠4,求证:AB∥CD.

证明:∵AD∥BC(已知)
∴∠3=∠______( )
又∵∠3=∠4(已知)
∴∠4=∠______( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(等式性质)
即∠BAF=∠_______
∴∠4=∠________( )
∴AB∥CD( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列四幅图象近似刻画两个变量之间的关系,请按图象顺序将下面四种情景与之对应排序( ).
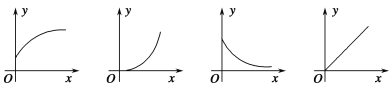
①一辆汽车在公路上匀速行驶(汽车行驶的路程与时间的关系)
②向锥形瓶中匀速注水(水面的高度与注水时间的关系)
③将常温下的温度计插入一杯热水中(温度计的读数与时间的关系)
④一杯越来越凉的水(水温与时间的关系)
A.①②④③ B.③④②①
C.①④②③ D.③②④①
查看答案和解析>>
科目:初中数学 来源: 题型:
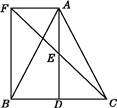
【题目】如图,△ABC中,D是BC边上的一点,E为AD的中点,过A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com