[题目]如图.在Rt△ABC中.∠C＝90°.斜边AB的垂直平分线交AB于点D.交BC于点E.AE平分∠BAC.那么下列不成立的是( )A.∠B＝∠CAEB.∠DEA＝∠CEAC.∠B＝∠BAED.AC＝2EC 题目和参考答案——青夏教育精英家教网—

【题目】如图，在Rt△ABC中，∠C＝90°，斜边AB的垂直平分线交AB于点D，交BC于点E，AE平分∠BAC，那么下列不成立的是（）

A.∠B＝∠CAEB.∠DEA＝∠CEAC.∠B＝∠BAED.AC＝2EC

【答案】D

【解析】

根据线段垂直平分线的性质，AE=BE，则∠B=∠CAE，再由AE平分∠BAC，得∠BAE=∠CAE．从而得出答案．

解：A、∵ED⊥AB，且BD=AD
∴∠B=∠DAE
又∵AE平分∠BAC，
∴∠CAE=∠DAE
故∠B=∠CAE．正确；
B、在△ADE与△ACE中，∠CAE=∠DAE，∠C=∠ADE=90°，
根据三角形内角和定理∠DEA=∠CEA．正确；
C、∵ED⊥AB，且BD=AD，∴∠B=∠BAE，正确；
D、不一定成立．
故选：D．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】如图，将Rt△ABO放在平面直角坐标系中，点A、B分别在y轴、x轴上，∠BAO＝30°，BC是∠ABO的角平分线，交y轴于点C（0，﹣2），CD⊥AB，垂足为D

（1）求BC的长度．

（2）点P（0，n）是线段AO上的任意一点（点P不与A、C、O重合），以BP为边，在BD的下方画出∠BPE＝60°，PE交CD的延长线于点E，在备用图中画出图形，并求CE的长（用含n的式子表示）．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】（1）操作：如图，在已知内角度数的三个三角形中，请用直尺从某一顶点画一条线段，把原三角形分割成两个等腰三角形，并在图中标注相应的角的度数

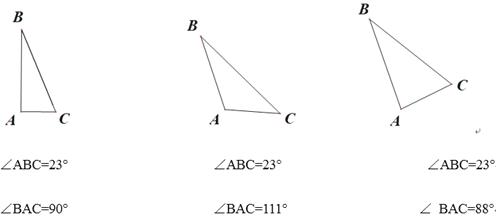
（2）拓展，△ABC中，AB=AC，∠A=45°，请把△ABC分割成三个等腰三角形，并在图中标注相应的角的度数.

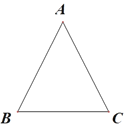
（3）思考在如图所示的三角形中∠A=30°.点P和点Q分别是边AC和BC上的两个动点.分别连接BP和PQ把△ABC分割成三个三角形.△ABP，△BPQ，△PQC若分割成的这三个三角形都是等腰三角形，求∠C的度数所有可能值直接写出答案即可.

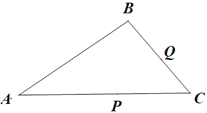
查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x=2，下列结论：（1）4a+b=0；（2）9a+c＞3b；（3）8a+7b+2c＞0；（4）若点A（﹣3，y1）、点B（﹣，y2）、点C（，y3）在该函数图象上，则y1＜y3＜y2；（5）若方程a（x+1）（x﹣5）=﹣3的两根为x1和x2，且x1＜x2，则x1＜﹣1＜5＜x2．其中正确的结论有（　　）