Question

【题目】如图，将Rt△ABO放在平面直角坐标系中，点A、B分别在y轴、x轴上，∠BAO＝30°，BC是∠ABO的角平分线，交y轴于点C（0，﹣2），CD⊥AB，垂足为D

（1）求BC的长度．

（2）点P（0，n）是线段AO上的任意一点（点P不与A、C、O重合），以BP为边，在BD的下方画出∠BPE＝60°，PE交CD的延长线于点E，在备用图中画出图形，并求CE的长（用含n的式子表示）．

Answer 1

【答案】（1）BC＝4；（2） EC＝2﹣n．

【解析】

（1）根据已知条件可知OC=2, Rt△BOC中，∠OBC＝∠DBC＝30°，BC＝2OC即可得出答案；（2）分两种情况，当点P在线段OC上时，在BC上取一点F，使得PF＝PC。证明△PCF是等边三角形，得出∠PCE＝∠PFB＝120°，然后证明△EPC≌△BPF，得到CE＝FB，再根据P点的坐标知道0P=-n,，PC=CF=2-(-n)=2+n,CE=BF=BC-CF计算即可；当点P在线段AC上时，在BC的延长线上取一点G，使得PG＝CP，同理可证. △PCG是等边三角形, △EPC≌△BPG,可得出CE＝GB＝BC+CF，再代入n计算即可.

（1）∵点C（0，﹣2），

∴OC＝2，

在Rt△ABO中，∵∠BAO＝30°，BC是∠ABO的平分线，∠BOC＝90°，

∴∠OBC＝∠DBC＝30°，

∴BC＝2OC＝4．

（2）∵P（0，n），

∴OP＝﹣n，

①如图1中，当点P在线段OC上时，在BC上取一点F，使得PF＝PC．

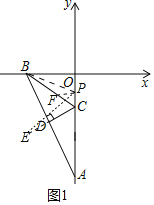
∵∠BOC＝90°，CD⊥AB，∠OBC＝∠DBC＝30°，

∴∠BCO＝∠BCE＝60°，

∵PF＝CF，

∴△PCF是等边三角形，

∴∠PFC＝∠FPC＝60°，PC＝CF，

∴∠BCO+∠BCE＝180°﹣∠PFC，即∠PCE＝∠PFB＝120°，

∵∠FPC＝∠BPE＝60°，

∴∠EPC＝∠BPF，

∴△EPC≌△BPF（ASA），

∴CE＝FB，

∵OP＝﹣n，

∴CF＝PC＝OC﹣OP＝2+n，

∴CE＝FB＝BC﹣CF＝4﹣（2+n）＝2﹣n．

②当点P在线段AC上时，在BC的延长线上取一点G，使得PG＝CP．

∵∠BCO＝∠BCE＝60°，

∴∠PCG＝∠BCO＝60°，∠PCE＝∠180°﹣60°﹣60°＝60°，

∵PG＝CP，

∴△PCG是等边三角形，

∴∠PGC＝∠GPC＝60°，PC＝CG，即∠PCE＝∠PGB，

∵∠BPE＝∠GPC＝60°，

∴∠EPC＝∠BPG，

∴△EPC≌△BPG（ASA），

∴CE＝GB，

∵OP＝﹣n，

∴CG＝PC＝OP﹣OC＝﹣n﹣2，

∴CE＝GB＝BC+CF＝4+（﹣n﹣2）＝2﹣n，

综上所述，EC＝2﹣n．