Question

【题目】已知点 C为线段 AB上一点，分别以 AC、BC为边在线段 AB同侧作△ACD和△BCE，且 CA＝CD，CB＝CE，∠ACD＝∠BCE，直线 AE与 BD交于点 F

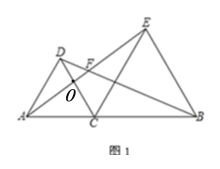
(1)如图 1，若∠ACD＝60°，则∠AFD＝

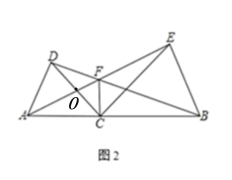
(2)如图 2，若∠ACD＝α，则∠AFB＝ （用含α的式子表示），并说明理由。

(3) 将图 1 中的△ACD绕点 C顺时针旋转如图 3，连接 AE、AB、BD，∠ABD＝80°，求∠EAB的度数.

Answer 1

【答案】（1）60°；（2）180°-α，理由见解析；（3）140°

【解析】

（1）求出∠ACE=∠DCB，证出△ACE≌△DCB，根据全等性质得出∠EAC=∠BDC,再根据三角形内角和定理求出即可；（2）证出△ACE≌△DCB，根据全等性质得出∠EAC=∠BDC,再根据三角形内角和定理求出∠AFD =α，再由补角性质求出∠AFB的度数；（3）由四边形内角和定理得出∠CAB+∠CDB=220°，再证出△ACE≌△DCB,根据全等三角形的性质得出∠CAE=∠CDB,再由周角性质求解.

解：（1）∠AFD =60°，理由如下：

如图1，设CD与AE交于点O,

∵CA＝CD，CB＝CE，∠ACD＝∠BCE，

∴∠ACE=∠DCB,

∴△ACE≌△DCB,

∴∠EAC=∠BDC,

∵∠DOF=∠AOC, ∠DOF+∠BDC+∠AFD=∠AOC+∠EAC+∠ACD,

∴∠AFD=∠ACD=60°,

即∠AFD =60°；

（2）∠AFB=180°-α，理由如下：

如图2，设CD与AE交于点O,

∵CA＝CD，CB＝CE，∠ACD＝∠BCE=α，

∴∠ACE=∠DCB,

∴△ACE≌△DCB,

∴∠EAC=∠BDC,

∵∠DOF=∠AOC, ∠DOF+∠BDC+∠AFD=∠AOC+∠EAC+∠ACD,

∴∠AFD=∠ACD=α,

即∠AFD =α；

∴∠AFB=180°-α

（3）∵△ACD是等边三角形，

∴∠ACD=60°,

∵∠ABD=80°,

∴∠CAB+∠CDB=360°-60°-80°=220°,

∵∠ACD=∠BCE,

∴∠ACE=∠BCD,

∵CE=BC,AC=CD,

∴△ACE≌△DCB,

∴∠CAE=∠CDB,

∴∠CAB+∠CAE=220°,

∴∠EAB=140°.