
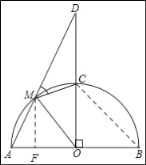
【题目】如图,AB是以O为圆心的半圆的直径,半径CO⊥AO,点M是![]() 上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
(1)若半圆的半径为10.
①当∠AOM=60°时,求DM的长;
②当AM=12时,求DM的长.
(2)探究:在点M运动的过程中,∠DMC的大小是否为定值?若是,求出该定值;若不是,请说明理由.

【答案】(1)①DM= 10;②MD=![]() ;(2)∠CMD=45°.
;(2)∠CMD=45°.
【解析】
(1)①当![]() 时,所以△AMO是等边三角形,从而可知∠MOD=30°,∠D=30°,所以DM=OM=10;
时,所以△AMO是等边三角形,从而可知∠MOD=30°,∠D=30°,所以DM=OM=10;
②过点M作MF⊥OA于点F,设AF=x,![]() 利用勾股定理即可求出x的值.易证明△AMF∽△ADO,从而可知AD的长度,进而可求出MD的长度.
利用勾股定理即可求出x的值.易证明△AMF∽△ADO,从而可知AD的长度,进而可求出MD的长度.
(2)根据点M的位置分类讨论,然后利用圆周角定理以及圆内接四边形的性质即可求出答案.
(1)①当∠AOM=60°时,
∵![]()
∴△AMO是等边三角形,
∴∠A=∠MOA=60°,
∴∠MOD=30°,∠D=30°,
∴DM=OM=10
②过点M作MF⊥OA于点F,
设![]()
∴![]()
∵![]()
由勾股定理可知:![]()
∴![]()
∴![]()
∵MF∥OD,
∴△AMF∽△ADO,
∴![]()
![]()
![]()
∴![]()
∴![]()
(2)当点M位于![]() 之间时,
之间时,
连接BC,
∵C是![]() 的中点,
的中点,
∴∠B=45°,
∵四边形AMCB是圆内接四边形,
此时∠CMD=∠B=45°,
当点M位于![]() 之间时,
之间时,
连接BC,
由圆周角定理可知:∠CMD=∠B=45°
综上所述,∠CMD=45°



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】暑假到了,即将迎来手机市场的销售旺季.某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示:
甲 | 乙 | |
进价(元/部) | 4000 | 2500 |
售价(元/部) | 4300 | 3000 |
该商场计划投入15.5万元资金,全部用于购进两种手机若干部,期望全部销售后可获毛利润不低于2万元.(毛利润=(售价﹣进价)×销售量)
(1)若商场要想尽可能多的购进甲种手机,应该安排怎样的进货方案购进甲乙两种手机?
(2)通过市场调研,该商场决定在甲种手机购进最多的方案上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC的边AB,AC的外侧分别作等边△ABD和等边△ACE,连接DC,BE.
(1)求证:DC=BE;
(2)若BD=3,BC=4, BD⊥BC于点B,请求出△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小柔要榨果汁,她有苹果、芭乐、柳丁三种水果,且其颗数比为9:7:6,小柔榨完果汁后,苹果、芭乐、柳丁的颗数比变为6:3:4,已知小柔榨果汁时没有使用柳丁,关于她榨果汁时另外两种水果的使用情形,下列叙述何者正确?( )
A. 只使用苹果
B. 只使用芭乐
C. 使用苹果及芭乐,且使用的苹果颗数比使用的芭乐颗数多
D. 使用苹果及芭乐,且使用的芭乐颗数比使用的苹果颗数多
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O,A1;将C1绕点A1旋转180°得C2,交x轴于点A2;将C2绕点A2旋转180°得C3,交x轴于点A3;…如此进行下去,直至得C17.
(1)写出点![]() 的坐标________
的坐标________
(2)若P(50,m)在第17段抛物线C17上,则m=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、F、G.
(1)点F到△ABC的边_______的距离相等,点F到△ABC的顶点______的距离相等.
(2)若BC=6,AD=9,求AF的值.
(3)连接CG交AD于点H,当∠BAC是多少度时,△FGH为等腰三角形?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 和
和![]() 的平分线相交于点
的平分线相交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() 下列结论:①
下列结论:①![]() ;②点
;②点![]() 到
到![]() 各边的距离相等;③
各边的距离相等;③![]() ;④设
;④设![]() ,
,![]() ,则
,则![]() ;⑤
;⑤![]() .其中正确的结论是.__________.
.其中正确的结论是.__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com