
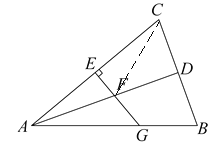
【题目】如图,在△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、F、G.
(1)点F到△ABC的边_______的距离相等,点F到△ABC的顶点______的距离相等.
(2)若BC=6,AD=9,求AF的值.
(3)连接CG交AD于点H,当∠BAC是多少度时,△FGH为等腰三角形?


【答案】(1)AC,AB;A、B、C;(2)5;(3)45°或36°.
【解析】
(1)根据等腰三角形性质,AD平分∠BAC,AD垂直平分BC,F在AD上,根据角平分线性质解答;EF垂直平分AC,所以F为两边垂直平分线的交点.根据垂直平分线性质解答.
(2)连接FC,根据垂直平分线的性质得到AF=CF,设AF=x,则CF=x,DF=9-x,CD=![]() BC=3,故利用Rt△FCD得到方程进行求解;
BC=3,故利用Rt△FCD得到方程进行求解;
(3)根据△FGH为等腰三角形分三种情况分别讨论,根据垂直平分线与三角形的内角和即可求解.
(1)∵AB=AC,D是BC的中点,
∴AD平分∠BAC,AD垂直平分BC.
∵点F在AD上,
∴点F到AC、AB的距离相等;
∵EF垂直平分AC,AD垂直平分BC.
∴FA=FB=FC,即点F到A、B、C的距离相等.
故答案为 AC、AB; A、B、C.
(2)连接FC,根据垂直平分线的性质得到AF=CF,
设AF=x,则CF=x,DF=9-x,CD=![]() BC=3,
BC=3,
在Rt△FCD中,![]()
即![]()
解得x=5,
故AF=5;
(3)①当FG=HG时,故∠GFH=∠GHF,
∵∠GFH=∠EFA,∠EFA+∠EAF=90°,
同理∠CHD+∠HCD=90°
∴∠EAF =∠HCD,
∵AD垂直平分BC,
∴∠EAF =∠BAD,
∴∠HCD=∠BAD
∵AD⊥BC,∠B=∠B
∴CG⊥AB,
又EG垂直平分AC,
∴AG=CG,
故∠BAC=45°,
②当FH=HG时,故∠HFG=∠HGF,
∵∠GFH=∠EFA,∠EFA+∠EAF=90°,
又∠HGF+∠ECG=90°
∴∠EAF=∠ECG
∵EG垂直平分AC,∴∠ECG=∠EAG
∴此情况不存在;
③当FH=FG时,故∠FHG=∠FGH
∵∠FHG =∠CHD,∠CHD+∠HCD=90°,
又∠HGF+∠ECG=90°
∴∠EAF=∠ECG
∴∠ECG =∠HCD,
∵AD垂直平分BC,
∴∠ECG =∠BAC
设∠BAC=a,故∠ACG=∠HCD=a,∠ACB=2a,
∵AB=AC,∴∠ABC=∠ACB=2a
故∠BAC+∠ABC+∠ACB=5a=180°,
解得x=36°,
综上:∠BAC是45°或36°时,△FGH为等腰三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】若整数a既使关于x的分式方程![]() 的解为正数,又使关于x的一元二次方程x2﹣2x+2a﹣5=0有实数解,则符合条件的所有a的和是( )
的解为正数,又使关于x的一元二次方程x2﹣2x+2a﹣5=0有实数解,则符合条件的所有a的和是( )
A. 0 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】海南建省30年来,各项事业取得令人瞩目的成就,以2016年为例,全省社会固定资产总投资约3730亿元,其中包括中央项目、省属项目、地(市)属项目、县(市)属项目和其他项目.图1、图2分别是这五个项目的投资额不完整的条形统计图和扇形统计图,请完成下列问题:
(1)在图1中,先计算地(市)属项目投资额为 亿元,然后将条形统计图补充完整;
(2)在图2中,县(市)属项目部分所占百分比为m%、对应的圆心角为β,则m= ,β= 度(m、β均取整数).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是以O为圆心的半圆的直径,半径CO⊥AO,点M是![]() 上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
(1)若半圆的半径为10.
①当∠AOM=60°时,求DM的长;
②当AM=12时,求DM的长.
(2)探究:在点M运动的过程中,∠DMC的大小是否为定值?若是,求出该定值;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为使中华传统文化教育更具有实效性,军宁中学开展以“我最喜爱的传统文化种类”为主题的调查活动,围绕“在诗词、国画、对联、书法、戏曲五种传统文化中,你最喜爱哪一种?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图,请你根据图中提供的信息回答下列问题:
(1)本次调查共抽取了多少名学生?
(2)通过计算补全条形统计图;
(3)若军宁中学共有960名学生,请你估计该中学最喜爱国画的学生有多少名?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠C=90°,点A、B分别在∠C的两直角边上,AC=1,BC=2.
判断:![]() 是 .(填“有理数”或“无理数”)
是 .(填“有理数”或“无理数”)
画图:人类经历了漫长、曲折的历史过程,发现了无理数是客观存在的.
(1)在图中画出长度为![]() 的线段,并说明理由;
的线段,并说明理由;
(2)在射线CA上画出长度为![]() 的线段.(注:保留画图痕迹,并把所画线段标注出来)
的线段.(注:保留画图痕迹,并把所画线段标注出来)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,OA是⊙O的半径,点D为OA上的一动点,过D作线段CD⊥OA交⊙O于点F,过点C作⊙O的切线BC,B为切点,连接AB,交CD于点E.
(1)求证:CB=CE;
(2)如图2,当点D运动到OA的中点时,CD刚好平分![]() ,求证:△BCE是等边三角形;
,求证:△BCE是等边三角形;
(3)如图3,当点D运动到与点O重合时,若⊙O的半径为2,且∠DCB=45°,求线段EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() ,
,![]() 分别是等边
分别是等边![]() 边
边![]() ,
,![]() 上的动点,点
上的动点,点![]() 从顶点
从顶点![]() 向点
向点![]() 运动,点
运动,点![]() 从顶点
从顶点![]() 向点
向点![]() 运动,两点同时出发,且它们的速度都相同.
运动,两点同时出发,且它们的速度都相同.
(1)连接![]() ,
,![]() 交于点
交于点![]() ,则在
,则在![]() ,
,![]() 运动的过程中,
运动的过程中,![]() 的大小发生变化吗?若变化,则说明理由,若不变,则求出它的度数;
的大小发生变化吗?若变化,则说明理由,若不变,则求出它的度数;
(2)如图2,若点![]() ,Q在运动到终点后继续在射线
,Q在运动到终点后继续在射线![]() ,
,![]() 上运动,直线
上运动,直线![]() 、
、![]() 交点为
交点为![]() ,则
,则![]() 的大小发生变化吗?若变化,则说明理由,若不变,则求出它的度数.
的大小发生变化吗?若变化,则说明理由,若不变,则求出它的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小磊要制作一个三角形的钢架模型,在这个三角形中,长度为x(单位:cm)的边与这条边上的高之和为40 cm,这个三角形的面积S(单位:cm2)随x(单位:cm)的变化而变化.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)当x是多少时,这个三角形面积S最大?最大面积是多少?![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com