
【题目】如图,在![]() 中,
中,![]() 和
和![]() 的平分线相交于点
的平分线相交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() 下列结论:①
下列结论:①![]() ;②点
;②点![]() 到
到![]() 各边的距离相等;③
各边的距离相等;③![]() ;④设
;④设![]() ,
,![]() ,则
,则![]() ;⑤
;⑤![]() .其中正确的结论是.__________.
.其中正确的结论是.__________.

【答案】①②③⑤
【解析】
由在△ABC中,∠ABC和∠ACB的平分线相交于点O,根据角平分线的定义与三角形内角和定理,即可求得③∠BOC=90°+![]() ∠A正确;由平行线的性质和角平分线的定义得出△BEO和△CFO是等腰三角形得出EF=BE+CF故①正确;由角平分线的性质得出点O到△ABC各边的距离相等,故②正确;由角平分线定理与三角形面积的求解方法,即可求得④设OD=m,AE+AF=n,则S△AEF=
∠A正确;由平行线的性质和角平分线的定义得出△BEO和△CFO是等腰三角形得出EF=BE+CF故①正确;由角平分线的性质得出点O到△ABC各边的距离相等,故②正确;由角平分线定理与三角形面积的求解方法,即可求得④设OD=m,AE+AF=n,则S△AEF=![]() mn,故④错误,根据HL证明△AMO≌△ADO得到AM=AD,同理可证BM=BN,CD=CN,变形即可得到⑤正确.
mn,故④错误,根据HL证明△AMO≌△ADO得到AM=AD,同理可证BM=BN,CD=CN,变形即可得到⑤正确.
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,∠A+∠ABC+∠ACB=180°,∴∠OBC+∠OCB=90°﹣
∠ACB,∠A+∠ABC+∠ACB=180°,∴∠OBC+∠OCB=90°﹣![]() ∠A,∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+
∠A,∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+![]() ∠A;故③正确;
∠A;故③正确;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴∠OBC=∠OBE,∠OCB=∠OCF.
∵EF∥BC,∴∠OBC=∠EOB,∠OCB=∠FOC,∴∠EOB=∠OBE,∠FOC=∠OCF,∴BE=OE,CF=OF,∴EF=OE+OF=BE+CF,故①正确;
过点O作OM⊥AB于M,作ON⊥BC于N,连接OA.
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴ON=OD=OM=m,∴S△AEF=S△AOE+S△AOF=![]() AEOM+
AEOM+![]() AFOD=
AFOD=![]() OD(AE+AF)=
OD(AE+AF)=![]() mn;故④错误;
mn;故④错误;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,∴点O到△ABC各边的距离相等,故②正确;
∵AO=AO,MO=DO,∴△AMO≌△ADO(HL),∴AM=AD;
同理可证:BM=BN,CD=CN.
∵AM+BM=AB,AD+CD=AC,BN+CN=BC,∴AD=![]() (AB+AC﹣BC)故⑤正确.
(AB+AC﹣BC)故⑤正确.
故答案为:①②③⑤.



 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是以O为圆心的半圆的直径,半径CO⊥AO,点M是![]() 上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
(1)若半圆的半径为10.
①当∠AOM=60°时,求DM的长;
②当AM=12时,求DM的长.
(2)探究:在点M运动的过程中,∠DMC的大小是否为定值?若是,求出该定值;若不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() ,
,![]() 分别是等边
分别是等边![]() 边
边![]() ,
,![]() 上的动点,点
上的动点,点![]() 从顶点
从顶点![]() 向点
向点![]() 运动,点
运动,点![]() 从顶点
从顶点![]() 向点
向点![]() 运动,两点同时出发,且它们的速度都相同.
运动,两点同时出发,且它们的速度都相同.
(1)连接![]() ,
,![]() 交于点
交于点![]() ,则在
,则在![]() ,
,![]() 运动的过程中,
运动的过程中,![]() 的大小发生变化吗?若变化,则说明理由,若不变,则求出它的度数;
的大小发生变化吗?若变化,则说明理由,若不变,则求出它的度数;
(2)如图2,若点![]() ,Q在运动到终点后继续在射线
,Q在运动到终点后继续在射线![]() ,
,![]() 上运动,直线
上运动,直线![]() 、
、![]() 交点为
交点为![]() ,则
,则![]() 的大小发生变化吗?若变化,则说明理由,若不变,则求出它的度数.
的大小发生变化吗?若变化,则说明理由,若不变,则求出它的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,点D是AC的中点,作∠ADB的角平分线DE交AB于点E,
(1)求证:DE∥BC;
(2)若AE=3,AD=5,点P为线段BC上的一动点,当BP为何值时,△DEP为等腰三角形.请求出所有BP的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() 、
、![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是直线
是直线![]() 上的一个动点.
上的一个动点.

(1)求![]() 的值;
的值;
(2)点![]() 在第二象限内的直线
在第二象限内的直线![]() 上的运动过程中,写出
上的运动过程中,写出![]() 的面积
的面积![]() 与
与![]() 的函整表达式,并写出自变量
的函整表达式,并写出自变量![]() 的取值范围;
的取值范围;
(3)探究,当点![]() 在直线
在直线![]() 上运动到时,
上运动到时,![]() 的面积可能是
的面积可能是![]() 吗,若能,请求出点
吗,若能,请求出点![]() 的坐标;若不能,说明理由.
的坐标;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
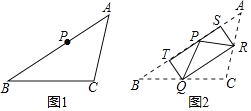
【题目】如图所示,图1为三角形纸片ABC,点P在AB上.若将纸片向内折叠,如图2所示,点A、B、C恰能重合在点P处,折痕分别为SR、RQ、QT,折痕的交点R、Q分别在边AC、BC上.若△ABC、四边形PTQR的面积分别是20和7,则△RPS的面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小磊要制作一个三角形的钢架模型,在这个三角形中,长度为x(单位:cm)的边与这条边上的高之和为40 cm,这个三角形的面积S(单位:cm2)随x(单位:cm)的变化而变化.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)当x是多少时,这个三角形面积S最大?最大面积是多少?![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=20°,∠ABC与∠ACB的平分线交于点D1,∠ABD1与∠ACD1的平分线交于点D2,以此类推,∠ABD2与∠ACD2的平分线交于点D,则∠BDC的度数是__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点O是等边三角形ABC内一点,∠AOB=100°,∠BOC=α,D是△ABC外一点,且△ADC≌△BOC,连接OD.
(1)求证:△COD是等边三角形;
(2)当α=150°时,判断△AOD的形状,并说明理由。
(3)探究:当α=_____度时,△AOD是等腰三角形。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com