
【题目】利用“同角的余角相等”可以帮助我们得到相等的角,这个规律在全等三角形的判定中有着广泛的运用.
(1)如图①,![]() ,
,![]() ,
,![]() 三点共线,
三点共线,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() ,且
,且![]() .若
.若![]() ,求
,求![]() 的长.
的长.
(2)如图②,在平面直角坐标系中,![]() 为等腰直角三角形,直角顶点
为等腰直角三角形,直角顶点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .求直线
.求直线![]() 与
与![]() 轴的交点坐标.
轴的交点坐标.
(3)如图③,![]() ,
,![]() 平分
平分![]() ,若点
,若点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() .则
.则![]() .(只需写出结果,用含
.(只需写出结果,用含![]() ,
,![]() 的式子表示)
的式子表示)

【答案】(1)6;(2)(0,2);(3)![]()
【解析】
(1)利用AAS证出△ABC≌△CDE,根据全等三角形的性质可得AB=CD,BC=DE,再根据BD=CD+BC等量代换即可求出BD;
(2)过点A作AD⊥x轴于D,过点B作BE⊥x轴于E,利用AAS证出△ADC≌△CEB,根据全等三角形的性质可得AD=CE,CD=BE,根据点A和点C的坐标即可求出点B的坐标,然后利用待定系数法求出直线AB的解析式,即可求出直线AB与y轴的交点坐标;
(3)过点C作CD⊥y轴于D,CE⊥x轴于E,根据正方形的判定可得四边形OECD是正方形,然后利用ASA证出△DCA≌△ECB,从而得出DA=EB,S△DCA=S△ECB,然后利用正方形的边长相等即可求出a、b表示出DA和正方形的边长OD,然后根据![]() 即可推出
即可推出![]() =
=![]() ,最后求正方形的面积即可.
,最后求正方形的面积即可.
解:(1)∵![]() ,
,![]() ,
,![]()
∴∠ABC=∠CDE=∠ACE=90°
∴∠A+∠ACB=90°,∠ECD+∠ACB=180°-∠ACE=90°
∴∠A=∠ECD
在△ABC和△CDE中
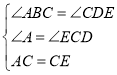
∴△ABC≌△CDE
∴AB=CD,BC=DE
∴BD=CD+BC=![]()
(2)过点A作AD⊥x轴于D,过点B作BE⊥x轴于E
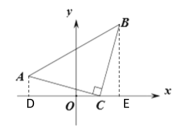
∵△ABC为等腰直角三角形
∴∠ADC=∠CEB=∠ACB=90°,AC=CB
∴∠DAC+∠ACD=90°,∠ECB+∠ACD=180°-∠ACB=90°
∴∠DAC =∠ECB
在△ADC和△CEB中
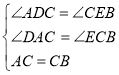
∴△ADC≌△CEB
∴AD=CE,CD=BE
∵点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]()
∴CO=1,AD=1,DO=2,
∴OE=OC+CE= OC+AD=2,BE=CD=CO+DO=3,
∴点B的坐标为(2,3)
设直线AB的解析式为y=kx+b
将A、B两点的坐标代入,得
![]()
解得:![]()
∴直线AB的解析式为![]()
当x=0时,解得y=2
∴直线![]() 与
与![]() 轴的交点坐标为(0,2);
轴的交点坐标为(0,2);
(3)过点C作CD⊥y轴于D,CE⊥x轴于E
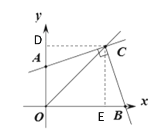
∵OC平分∠AOB
∴CD=CE
∴四边形OECD是正方形
∴∠DCE=90°,OD=OE
∵∠ACB=90°
∴∠DCA+∠ACE=∠ECB+∠ACE=90°
∴∠DCA=∠ECB
在△DCA和△ECB中
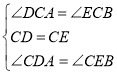
∴△DCA≌△ECB
∴DA=EB,S△DCA=S△ECB
∵点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]()
∴OB=b,OA=a
∵OD=OE
∴OA+DA=OB-BE
即a+DA=b-DA
∴DA=![]()
∴OD= OA+DA=![]()
![]()
=![]()
=![]()
= DA2
=![]()
=![]()
故答案为:![]() .
.


科目:初中数学 来源: 题型:
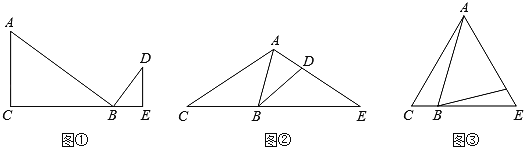
【题目】已知,点B在线段CE上.
(感知)(1)如图①,∠C=∠ABD=∠E=90°,易知△ACB∽△AED(不要求证明);
(拓展)(2)如图②,△ACE中,AC=AE,且∠ABD=∠E,求证:△ACB∽△BED;
(应用)(3)如图③,△ACE为等边三角形,且∠ABD=60°,AC=6,BC=2,则△ABD与△BDE的面积比为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
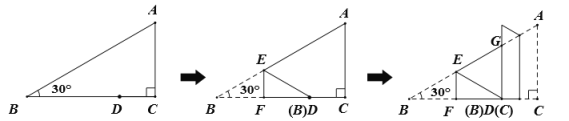
【题目】在三角形纸片![]() 中,
中,![]() ,
,![]() ,点
,点![]() (不与
(不与![]() ,
,![]() 重合)是
重合)是![]() 上任意一点,将此三角形纸片按下列方式折叠,若
上任意一点,将此三角形纸片按下列方式折叠,若![]() 的长度为
的长度为![]() ,则
,则![]() 的周长为__________.(用含
的周长为__________.(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
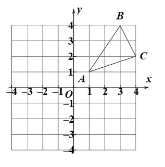
【题目】如图,在平面直角坐标系中,![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() ,
,![]() ,
,![]() .
.
(1)在图中画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(2)通过平移,使![]() 移动到原点
移动到原点![]() 的位置,画出平移后的
的位置,画出平移后的![]() .
.
(3)在![]() 中有一点
中有一点![]() ,则经过以上两次变换后点
,则经过以上两次变换后点![]() 的对应点
的对应点![]() 的坐标为 .
的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.

(1)求证:△ABM∽△EFA;
(2)若AB=12,BM=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有两辆玩具车进行30米的直跑道比赛,两车从起点同时出发,A车到达终点时,B车离终点还差12米,A车的平均速度为2.5米/秒.
(1)求B车的平均速度;
(2)如果两车重新比赛,A车从起点退后12米,两车能否同时到达终点?请说明理由;
(3)在(2)的条件下,若调整A车的平均速度,使两车恰好同时到达终点,求调整后A车的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,李老师出示了如下的题目:如图1,在等边![]() 中,点
中,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,试确定线段
,试确定线段![]() 与
与![]() 的大小关系,并说明理由,
的大小关系,并说明理由,
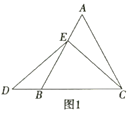
(1)小敏与同桌小聪探究解答的思路如下:
①特殊情况,探索结论,
当点![]() 为
为![]() 的中点时,如图2,确定线段
的中点时,如图2,确定线段![]() 与
与![]() 的大小关系,请你直接写出结论:
的大小关系,请你直接写出结论:![]() ______
______![]() .(填>,<或=)
.(填>,<或=)
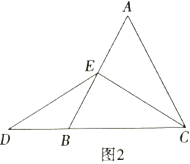
②特例启发,解答题目,
解:题目中,![]() 与
与![]() 的大小关系是:
的大小关系是:![]() ______
______![]() .(填>,<或=)
.(填>,<或=)
理由如下:如图3,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,(请你补充完成解答过程)
,(请你补充完成解答过程)
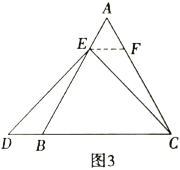
(2)拓展结论,设计新题,
同学小敏解答后,提出了新的问题:在等边![]() 中,点
中,点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 上,且
上,且![]() ,已知
,已知![]() 的边长为
的边长为![]() ,求
,求![]() 的长?(请直接写出结果)
的长?(请直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com