
【题目】已知,点B在线段CE上.
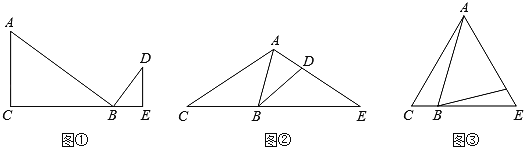
(感知)(1)如图①,∠C=∠ABD=∠E=90°,易知△ACB∽△AED(不要求证明);
(拓展)(2)如图②,△ACE中,AC=AE,且∠ABD=∠E,求证:△ACB∽△BED;
(应用)(3)如图③,△ACE为等边三角形,且∠ABD=60°,AC=6,BC=2,则△ABD与△BDE的面积比为 .
【答案】(1)见解析;(2)见解析;(3)7:2
【解析】
(1)由∠C=∠ABD=∠E=90°知∠A+∠ABC=∠ABC+∠DBE=90°,据此得∠A=∠DBE,从而得证.
(2)由∠C=∠ABD=∠E与∠ABE=∠C+∠CAB,∠ABE=∠ABD+∠DBE,即可求得∠CAB=∠DBE,即可证得:△ACB∽△BED.
(3)由△ACB∽△BED,根据相似三角形的对应边成比例,可求得△ABC与△BDE的面积比,△ABC与△ABE的面积比,继而求得答案.
(1)∵∠C=∠ABD=∠E=90°,
∴∠A+∠ABC=∠ABC+∠DBE=90°,
∴∠A=∠DBE,
∴△ACB∽△BED;
(2)∵AC=AE,
∴∠C=∠E,
∵∠ABD=∠E,
∴∠C=∠ABD,
又∵∠ABE=∠C+∠CAB,∠ABE=∠ABD+∠DBE,
∴∠CAB=∠DBE,
∴△ACB∽△BED;
(3)∵∠ABE=∠C+∠CAB,∠ABE=∠ABD+∠DBE,∠C=∠ABD,
∴∠CAB=∠DBE,
∵∠C=∠E=60°,
∴△ACB∽△BED,△ACE是等边三角形,
∴AE=AC=6,
∴BE=CE﹣BC=4,
∴△ACB与△BED的相似比为:3:2,
∴S△ABC:S△BED=9:4,S△ABC:S△ABE=1:2=9:18,
设S△ABC=9x,则S△ABE=18x,S△BDE=4x,
∴S△ABD=S△ABE﹣S△BED=18x﹣4x=14x,
∴S△ABD:S△BDE=14:4=7:2.
故答案为:7:2.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,以点
,以点![]() 为圆心,8为半径的圆与
为圆心,8为半径的圆与![]() 轴交于
轴交于![]() ,
,![]() 两点,过
两点,过![]() 作直线
作直线![]() 与
与![]() 轴负方向相交成
轴负方向相交成![]() 的角,且交
的角,且交![]() 轴于
轴于![]() 点,以点
点,以点![]() 为圆心的圆与
为圆心的圆与![]() 轴相切于点
轴相切于点![]() .
.

(1)求直线![]() 的解析式;
的解析式;
(2)将![]() 以每秒1个单位的速度沿
以每秒1个单位的速度沿![]() 轴向左平移,当
轴向左平移,当![]() 第一次与
第一次与![]() 外切时,求
外切时,求![]() 平移的时间.
平移的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一长方形纸片![]() 放在平面直角坐标系中,
放在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发以每秒1个单位长度的速度沿
出发以每秒1个单位长度的速度沿![]() 向终点
向终点![]() 运动,运动
运动,运动![]() 秒时,动点
秒时,动点![]() 从点
从点![]() 出发以相同的速度沿
出发以相同的速度沿![]() 向终点
向终点![]() 运动,当点
运动,当点![]() 、
、![]() 其中一点到达终点时,另一点也停止运动.
其中一点到达终点时,另一点也停止运动.
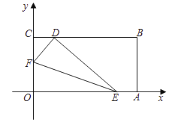
设点![]() 的运动时间为
的运动时间为![]() :(秒)
:(秒)
(1)![]() _________,
_________,![]() ___________(用含
___________(用含![]() 的代数式表示)
的代数式表示)
(2)当![]() 时,将
时,将![]() 沿
沿![]() 翻折,点
翻折,点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处,求点
处,求点![]() 的坐标及直线
的坐标及直线![]() 的解析式;
的解析式;
(3)在(2)的条件下,点![]() 是射线
是射线![]() 上的任意一点,过点
上的任意一点,过点![]() 作直线
作直线![]() 的平行线,与
的平行线,与![]() 轴交于
轴交于![]() 点,设直线
点,设直线![]() 的解析式为
的解析式为![]() ,当点
,当点![]() 与点
与点![]() 不重合时,设
不重合时,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
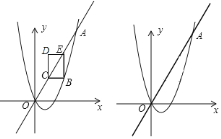
【题目】如图,已知抛物线![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() .
.
![]() 求抛物线的解析式.
求抛物线的解析式.
![]() 点
点![]() 是抛物线上
是抛物线上![]() 、
、![]() 之间的一个动点,过点
之间的一个动点,过点![]() 分别作
分别作![]() 轴、
轴、![]() 轴的平行线与直线
轴的平行线与直线![]() 交于点
交于点![]() 、
、![]() ,以
,以![]() 、
、![]() 为边构造矩形
为边构造矩形![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,求
,求![]() ,
,![]() 之间的关系式.
之间的关系式.
![]() 将射线
将射线![]() 绕原点逆时针旋转
绕原点逆时针旋转![]() 后与抛物线交于点
后与抛物线交于点![]() ,求
,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自动化车间计划生产480个零件,当生产任务完成一半时,停止生产进行自动化程序软件升级,用时20分钟,恢复生产后工作效率比原来提高了![]() ,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
,结果完成任务时比原计划提前了40分钟,求软件升级后每小时生产多少个零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用“同角的余角相等”可以帮助我们得到相等的角,这个规律在全等三角形的判定中有着广泛的运用.
(1)如图①,![]() ,
,![]() ,
,![]() 三点共线,
三点共线,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,![]() ,且
,且![]() .若
.若![]() ,求
,求![]() 的长.
的长.
(2)如图②,在平面直角坐标系中,![]() 为等腰直角三角形,直角顶点
为等腰直角三角形,直角顶点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .求直线
.求直线![]() 与
与![]() 轴的交点坐标.
轴的交点坐标.
(3)如图③,![]() ,
,![]() 平分
平分![]() ,若点
,若点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() .则
.则![]() .(只需写出结果,用含
.(只需写出结果,用含![]() ,
,![]() 的式子表示)
的式子表示)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com