
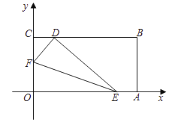
【题目】如图,将一长方形纸片![]() 放在平面直角坐标系中,
放在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发以每秒1个单位长度的速度沿
出发以每秒1个单位长度的速度沿![]() 向终点
向终点![]() 运动,运动
运动,运动![]() 秒时,动点
秒时,动点![]() 从点
从点![]() 出发以相同的速度沿
出发以相同的速度沿![]() 向终点
向终点![]() 运动,当点
运动,当点![]() 、
、![]() 其中一点到达终点时,另一点也停止运动.
其中一点到达终点时,另一点也停止运动.
设点![]() 的运动时间为
的运动时间为![]() :(秒)
:(秒)
(1)![]() _________,
_________,![]() ___________(用含
___________(用含![]() 的代数式表示)
的代数式表示)
(2)当![]() 时,将
时,将![]() 沿
沿![]() 翻折,点
翻折,点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处,求点
处,求点![]() 的坐标及直线
的坐标及直线![]() 的解析式;
的解析式;
(3)在(2)的条件下,点![]() 是射线
是射线![]() 上的任意一点,过点
上的任意一点,过点![]() 作直线
作直线![]() 的平行线,与
的平行线,与![]() 轴交于
轴交于![]() 点,设直线
点,设直线![]() 的解析式为
的解析式为![]() ,当点
,当点![]() 与点
与点![]() 不重合时,设
不重合时,设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
【答案】(1)6-t,t+![]() ;(2)D(1,3),y=
;(2)D(1,3),y=![]() x+
x+![]() ;(3)
;(3)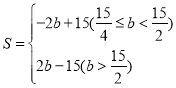
【解析】
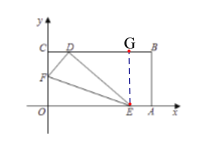
(1)根据点E,F的运动轨迹和速度,即可得到答案;
(2)由题意得:DF=OF=![]() ,DE=OE=5,过点E作EG⊥BC于点G,根据勾股定理得DG=4,进而得D(1,3),根据待定系数法,即可得到答案;
,DE=OE=5,过点E作EG⊥BC于点G,根据勾股定理得DG=4,进而得D(1,3),根据待定系数法,即可得到答案;
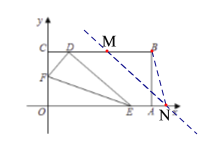
(3)根据题意得直线直线![]() 的解析式为:
的解析式为:![]() ,从而得M(
,从而得M(![]() ,3),分2种情况:①当点M在线段DB上时, ②当点M在DB的延长线上时,分别求出
,3),分2种情况:①当点M在线段DB上时, ②当点M在DB的延长线上时,分别求出![]() 与
与![]() 之间的函数关系式,即可.
之间的函数关系式,即可.
∵![]() ,
,![]() ,
,![]() ,
,
∴OA=6,OC=3,
∵AE=t×1= t,
∴![]() 6-t,
6-t,![]() (t+
(t+![]() )×1=t+
)×1=t+![]() ,
,
故答案是:6-t,t+![]() ;
;
(2)当![]() 时,
时,![]() 6-t=5,
6-t=5,![]() t+
t+![]() =
=![]() ,
,
∵将![]() 沿
沿![]() 翻折,点
翻折,点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处,
处,
∴DF=OF=![]() ,DE=OE=5,
,DE=OE=5,
过点E作EG⊥BC于点G,则EG=OC=3,CG=OE=5,
∴DG=![]() ,
,
∴CD=CG-DG=5-4=1,
∴D(1,3),
设直线![]() 的解析式为:y=kx+b,
的解析式为:y=kx+b,
把D(1,3),E(5,0)代入y=kx+b,得![]() ,解得:
,解得: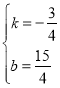 ,
,
∴直线![]() 的解析式为:y=
的解析式为:y=![]() x+
x+![]() ;
;
(3)∵MN∥DE,
∴直线直线![]() 的解析式为:
的解析式为:![]() ,
,
令y=3,代入![]() ,解得:x=
,解得:x=![]() ,
,
∴M(![]() ,3).
,3).
①当点M在线段DB上时,BM=6-(![]() )=
)=![]() ,
,
∴![]() =
=![]() ,
,
②当点M在DB的延长线上时,BM=![]() -6=
-6=![]() ,
,
∴![]() =
=![]() ,
,
综上所述: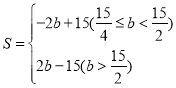 .
.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
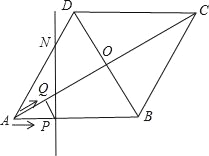
【题目】如图,菱形ABCD的边长为20cm,∠ABC=120°.动点P、Q同时从点A出发,其中P以4cm/s的速度,沿A→B→C的路线向点C运动;Q以2![]() cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.
cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.
(1)在点P、Q运动过程中,请判断PQ与对角线AC的位置关系,并说明理由;
(2)若点Q关于菱形ABCD的对角线交点O的对称点为M,过点P且垂直于AB的直线l交菱形ABCD的边AD(或CD)于点N.
①当t为何值时,点P、M、N在一直线上?
②当点P、M、N不在一直线上时,是否存在这样的t,使得△PMN是以PN为一直角边的直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市用![]() 元购进某种干果后进行销售,由于销售状况良好,超市又调拨
元购进某种干果后进行销售,由于销售状况良好,超市又调拨![]() 元资金购进该种干果,购进干果的数量是第一次的
元资金购进该种干果,购进干果的数量是第一次的![]() 倍,但这次每干克的进价比第一次的进价提高了
倍,但这次每干克的进价比第一次的进价提高了![]() 元.
元.
(1)该种干果第一次的进价是每千克多少元?
(2)如果超市按每千克![]() 元的价格销售,当大部分干果售出后,余下的
元的价格销售,当大部分干果售出后,余下的![]() 千克按售价的
千克按售价的![]() 折售完,超市销售这种干果共盈利多少元?
折售完,超市销售这种干果共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°.
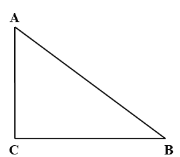
(1)作∠BAC的平分线,交BC于点D;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,若BD=5,CD=3,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工厂接到订单生产如图所示的巧克力包装盒子,每个盒子由3个长方形侧面和2个正三角形底面组成,仓库有甲、乙两种规格的纸板共2600张,其中甲种规格的纸板刚好可以裁出4个侧面(如图①),乙种规格的纸板可以裁出3个底面和2个侧面(如图②),裁剪后边角料(图中阴影部分)不再利用.
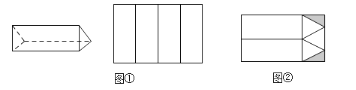
(1)若裁剪出的侧面和底面恰好全部用完,问两种规格的纸板各有多少张?
(2)一共能生产多少个巧克力包装盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程:![]() ;
;
(2)列分式方程解应用题:
用电脑程序控制小型赛车进行![]() 比赛,“畅想号”和“逐梦号”两赛车进入了最后的决赛.比赛中,两车从起点同时出发,“畅想号”到达终点时,“逐梦号”离终点还差
比赛,“畅想号”和“逐梦号”两赛车进入了最后的决赛.比赛中,两车从起点同时出发,“畅想号”到达终点时,“逐梦号”离终点还差![]() .从赛后数据得知两车的平均速度相差
.从赛后数据得知两车的平均速度相差![]() .求“畅想号”的平均速度.
.求“畅想号”的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把抛物线![]() 沿
沿![]() 轴向右平移
轴向右平移![]() 个单位后,再沿
个单位后,再沿![]() 轴翻折得到抛物线
轴翻折得到抛物线![]() 称为第一次操作,把抛物线
称为第一次操作,把抛物线![]() 沿
沿![]() 轴向右平移
轴向右平移![]() 个单位后,再沿
个单位后,再沿![]() 轴翻折得到抛物线
轴翻折得到抛物线![]() 称为第二次操作,…,以此类推,则抛物线
称为第二次操作,…,以此类推,则抛物线![]() 经过第
经过第![]() 此操作后得到的抛物线
此操作后得到的抛物线![]() 的解析式为( )
的解析式为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
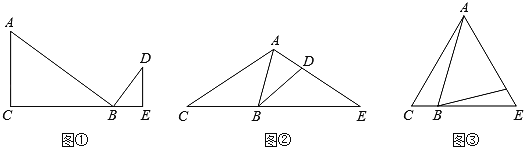
【题目】已知,点B在线段CE上.
(感知)(1)如图①,∠C=∠ABD=∠E=90°,易知△ACB∽△AED(不要求证明);
(拓展)(2)如图②,△ACE中,AC=AE,且∠ABD=∠E,求证:△ACB∽△BED;
(应用)(3)如图③,△ACE为等边三角形,且∠ABD=60°,AC=6,BC=2,则△ABD与△BDE的面积比为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com