
【题目】工厂接到订单生产如图所示的巧克力包装盒子,每个盒子由3个长方形侧面和2个正三角形底面组成,仓库有甲、乙两种规格的纸板共2600张,其中甲种规格的纸板刚好可以裁出4个侧面(如图①),乙种规格的纸板可以裁出3个底面和2个侧面(如图②),裁剪后边角料(图中阴影部分)不再利用.
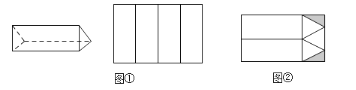
(1)若裁剪出的侧面和底面恰好全部用完,问两种规格的纸板各有多少张?
(2)一共能生产多少个巧克力包装盒?
【答案】(1)仓库有甲种规格的纸板1000张,有乙种规格的纸板1600张;(2)2400个.
【解析】
(1)设仓库有甲种规格的纸板x张,则有乙种规格的纸板(2600-x)张,根据“每个盒子由3个长方形侧面和2个正三角形底面组成,裁剪出的侧面和底面恰好全部用完”,列出方程,即可求解;
(2)由(1)求出裁得的长方形个数,进而即可得到答案.
(1)设仓库有甲种规格的纸板x张,则有乙种规格的纸板(2600-x)张,
根据题意得:4x+2(2600-x)=3(2600-x)×1.5,解得:x=1000,
2600-x=1600(张),
答:仓库有甲种规格的纸板1000张,有乙种规格的纸板1600张;
(2)当x=1000时,4x+2(2600-x)=7200(个),
7200÷3=2400(个),
答:一共能生产2400个巧克力包装盒.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】下列命题中正确的是( )
A. 有两条边相等的两个等腰三角形全等
B. 两腰对应相等的两个等腰三角形全等
C. 两角对应相等的两个等腰三角形全等
D. 一边对应相等的两个等边三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某汽车行驶的路程S(千米)与时间t(分)的函数关系图.观察图中所提供的信息,解答下列问题:
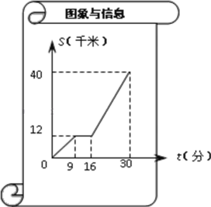
(1)汽车在前9分钟内的平均速度是______千米/分;
(2)当16≤t≤30时,求S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,设点P(x1,y1),Q(x2,y2)是图形W上的任意两点. 定义图形W的测度面积:若|x1-x2|的最大值为m,|y1-y2|的最大值为n,则S=mn为图形W的测度面积. 例如,若图形W是半径为l的⊙O. 当P,Q分别是⊙O与x轴的交点时,如图1,|x1-x2|取得最大值,且最大值m=2;当P,Q分别是⊙O与y轴的交点时,如图2,|y1-y2|取得最大值,且最大值n=2. 则图形W的测度而积S=mn=4.

(1)若图形W是抛物线y=-x2+2x+3和直线y=2x-1围成的封闭图形,则它的测度面积S=______

(2)若图形W是一个边长为1的正方形ABCD.
①当A,B两点均在x轴上时,它的测度面积S=_________;
②此图形测度面积S的最大值为_________;
(3)若图形W是一个边长分别为3和6的矩形ABCD,求它的测度面积S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中.点E,F分别在BC,CD上,△AEF是等边三角形.连接AC交EF于点G.过点G作GH⊥CE于点H.若![]() ,则
,则![]() =( )
=( )

A. 6 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD⊥BC于点D,AE平分∠DAC,∠B=50°,求∠DAE的度数为( )
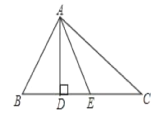
A.45°B.20°C.30°D.25°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=![]() ,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )
,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )

A. ![]() B. 3 C. 2 D. 2
B. 3 C. 2 D. 2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com