
【题目】解下列方程:
(1)3x(x﹣1)=2﹣2x;
(2)![]() ;
;
(3)先化简,后求值:(a2b)2(![]() )3÷(﹣
)3÷(﹣![]() )4,其中a=(
)4,其中a=(![]() ﹣
﹣![]() )0,b=(﹣
)0,b=(﹣![]() )﹣2.
)﹣2.
【答案】(1)x1=1,x2=﹣![]() ;(2)x1=﹣1,x2=﹣3;(3)﹣4.
;(2)x1=﹣1,x2=﹣3;(3)﹣4.
【解析】【试题分析】
(1)利用因式分解法解一元二次方程,3x(x﹣1)=2﹣2x,
移项得,3x(x﹣1)﹣2+2x=0;即3x(x﹣1)+2(x﹣1)=0;得(x﹣1)(3x+2)=0;
解得x1=1,x2=﹣![]() ;
;
(2)去分母得:方程两边同乘以x(x+3)得,
3=x(x+3)﹣x,即x(x+3)+(x+3)=0;因式分解得:(x﹣3)(x+1)=0;解得x1=﹣1,x2=﹣3;经验证x2=﹣3是原方程的增根舍去,x1=﹣1是原方程的解.(解分式方程一定要检验)
(3)∵(a2b)2(-![]() )3÷(﹣
)3÷(﹣![]() )4=﹣(a4b2)(
)4=﹣(a4b2)(![]() )
)![]() =﹣a2b,化简a=(
=﹣a2b,化简a=(![]() ﹣
﹣![]() )0=1,b=(﹣
)0=1,b=(﹣![]() )﹣2=4,则a=1,b=4;则原式=﹣4.
)﹣2=4,则a=1,b=4;则原式=﹣4.
【试题解析】
(1)∵3x(x﹣1)=2﹣2x,
移项得,3x(x﹣1)﹣2+2x=0
即3x(x﹣1)+2(x﹣1)=0
∴(x﹣1)(3x+2)=0
解得x1=1,x2=﹣![]() ;
;
(2)方程两边同乘以x(x+3)得,
3=x(x+3)﹣x,
即x(x+3)+(x+3)=0
∴(x﹣3)(x+1)=0
解得x1=﹣1,x2=﹣3;
经验证x2=﹣3是原方程的增根舍去,x1=﹣1是原方程的解.
(3)∵(a2b)2(-![]() )3÷(﹣
)3÷(﹣![]() )4=﹣(a4b2)(-
)4=﹣(a4b2)(-![]() ) (×
) (×![]() =﹣a2b,
=﹣a2b,
∴a=(![]() ﹣
﹣![]() )0=1,b=(﹣
)0=1,b=(﹣![]() )﹣2=4,
)﹣2=4,
∴a=1,b=4;
∴原式=﹣4.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项,现随机抽查了m名学生,并将其结果绘制成如下不完整的条形图和扇形图.

请结合以上信息解答下列问题:
(1)m= ;
(2)请补全上面的条形统计图;
(3)在图2中,“乒乓球”所对应扇形的圆心角的度数为 ;
(4)已知该校共有1200名学生,请你估计该校约有 名学生最喜爱足球活动.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数![]() (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京广高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的![]() ;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
;若由甲队先做10天,剩下的工程再由甲、乙两队合作30天完成.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.4万元,乙队每天的施工费用为5.6万元.工程预算的施工费用为500万元.为缩短工期并高效完成工程,拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?请给出你的判断并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
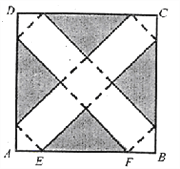
【题目】如图,在边长为24cm的正方形纸片ABCD上,剪去图中阴影部分的四个全等的等腰直角三角形,再沿图中的虚线折起,折成一个长方体形状的包装盒(A、B、C、D四个顶点正好重合于底面上一点).已知E、F在AB边上,是被剪去一个等腰直角三角形斜边的两个端点,设AE=BF=xcm.
(1)若折成的包装盒恰好是正方体,试求这个包装盒的体积V;
(2)某广告商要求包装盒的表面(不含下底面)面积S最大,试问x应取何值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是从一副扑克牌中取出的两组牌,分别是黑桃1,2,3,4和方块1,2,3,4,将它们背面朝上分别重新洗牌后,从两组牌中各摸出一张,那么摸出的两张牌的牌面数字之和等于5的概率是多少?请你用列举法(列表或画树状图)加以分析说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
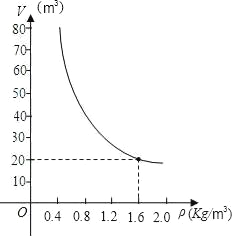
【题目】已知质量一定的某物体的体积V(m3)是密度ρ(kg/m3)的反比例函数,其图象如图所示:
(1)请写出该物体的体积V与密度ρ的函数关系式;
(2)当该物体的密度ρ=3.2Kg/m3时,它的体积v是多少?
(3)如果将该物体的体积控制在10m3~40m3之间,那么该物体的密度应在什么范围内变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工厂接到订单生产如图所示的巧克力包装盒子,每个盒子由3个长方形侧面和2个正三角形底面组成,仓库有甲、乙两种规格的纸板共2600张,其中甲种规格的纸板刚好可以裁出4个侧面(如图①),乙种规格的纸板可以裁出3个底面和2个侧面(如图②),裁剪后边角料(图中阴影部分)不再利用.
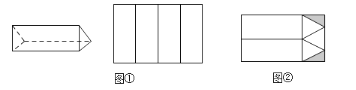
(1)若裁剪出的侧面和底面恰好全部用完,问两种规格的纸板各有多少张?
(2)一共能生产多少个巧克力包装盒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com