
【题目】下面有4个命题:①过任意三点可以画一个圆;②同圆的内接正方形和内接正三角形的边长比是![]() :
:![]() ;③三角形的内心到三角形的三边距离相等;④长度相等的弧是等弧.其中正确的有_____(填序号).
;③三角形的内心到三角形的三边距离相等;④长度相等的弧是等弧.其中正确的有_____(填序号).
【答案】②③.
【解析】
根据圆的定义可以判断①;分别计算出圆内接正方形和内接正三角形的边长判断②;根据三角形内心的定义判断③;根据等弧的定义可以判断④.
解:①过不在同一直线上的三点可以画一个圆,原说法错误;
②同圆的内接正方形和内接正三角形的边长比是![]()
如下图所示:
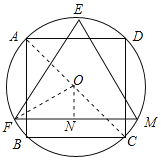
设圆的半径为R,在正方形ABCD中,连接AC,
∵∠B=90°,
∴AC为直径,
∴AC=2R,
∴AB=![]() AC=
AC=![]() R,
R,
在正三角形EFM中,作ON⊥FM于N,连接OF,
则∠ONF=90°,∠OFN=![]() ∠EFM=30°,
∠EFM=30°,
∴ON=![]() R,
R,
∴FN=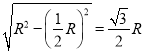 ,
,
∴FM=2FN=![]() R,
R,
∴AB:FM=![]() ,本说法正确;
,本说法正确;
③三角形的内心到三角形的三边距离相等,本说法正确;
④能够互相重合的弧是等弧,本说法错误,
故答案为:②③.


科目:初中数学 来源: 题型:
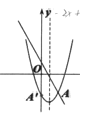
【题目】如图,已知直线y=-2x+1与抛物线y=x2-2x+c的一个交点为点A,作点A关于抛物线对称轴的对称点A,当A刚好落在y轴上时,c的值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
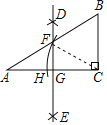
【题目】如图,在△ABC中,∠ACB=90°,分别以点A、C为圆心,以大于![]() AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( )
AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( )
A. ![]() B. 2C.
B. 2C. ![]() +1D. 2
+1D. 2![]() ﹣2
﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公园要建造一个圆形的喷水池,在水池中央垂直于水面竖一根柱子,上面的A处安装一个喷头向外喷水.连喷头在内,柱高0.8m.水流在各个方向上沿形状相同的抛物线路径落下,如图(1)所示.
根据设计图纸已知:如图(2)中所示直角坐标系中,水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是 y=﹣x2+2x+![]() .
.
(1)喷出的水流距水平面的最大高度是多少?
(2)如果不计其他因素,那么水池半径至少为多少时,才能使喷出的水流都落在水池内?
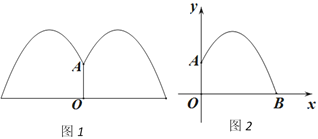
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】概念认识
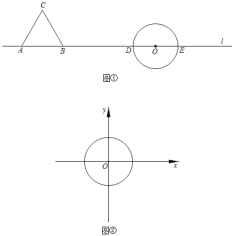
平面内,M为图形T上任意一点,N为⊙O上任意一点,将M、N两点间距离的最小值称为图形T到⊙O的“最近距离”,记作d(T﹣⊙O).例如图①,在直线l上有A、B、O三点,以AB为一边作等边△ABC,以点O为圆心作圆,与l交于D、E两点,若将△ABC记为图形T,则B、D两点间的距离称为图形T到⊙O的“最近距离”.
数学理解
(1)在直线l上有A、B两点,以点A为圆心,3为半径作⊙A,将点B记为图形T,若d(T﹣⊙A)=1,则AB= .
(2)如图②,在平面直角坐标系中,以O(0,0)为圆心,半径为2作圆.
①将点C(4,3)记为图形T,则d(T﹣⊙O)= .
②将一次函数y=kx+2![]() 的图记为图形T,若d(T﹣⊙O)>0,求k的取值范围.
的图记为图形T,若d(T﹣⊙O)>0,求k的取值范围.
推广运用
(3)在平面直角坐标系中,P的坐标为(t,0),⊙P的半径为2,D、E两点的坐标分别为(﹣8,8)、(﹣8,﹣8),将∠DOE记为图形T,若d(T﹣⊙P)=1,则t= .
查看答案和解析>>
科目:初中数学 来源: 题型:
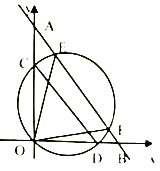
【题目】如图,在平面直角坐标系中,直线![]() 交y轴于点A,交x轴于点B,点C在线段OA上,点D在线段OB上,且
交y轴于点A,交x轴于点B,点C在线段OA上,点D在线段OB上,且![]() ,点C、D不与点O重合,以CD为直径的圆交直线AB于两点E、F,连接OE、OF,则当
,点C、D不与点O重合,以CD为直径的圆交直线AB于两点E、F,连接OE、OF,则当![]() 的面积的最大时,线段EF的长是________.
的面积的最大时,线段EF的长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]()
![]() 的顶点为(m
的顶点为(m![]() ,n
,n![]() )抛物线
)抛物线![]() 的顶点为(m
的顶点为(m![]() ,n
,n![]() ),如果
),如果![]() ,那么我们称抛物线
,那么我们称抛物线![]() 与
与![]() 关于点
关于点![]() 中心对称,给出抛物线①
中心对称,给出抛物线①![]() ;②
;②![]()
(1)判断抛物线①与抛物线②是否中心对称?若是,求出对称中心的坐标;若不是,说明理由;
(2)直线y=m交抛物线①于A. B两点,交抛物线②于C. D两点,如果AB=2CD,求m的值;
(3)设抛物线①与抛物线②的顶点分别为M、N,点P在x轴上移动,若△MNP为直角三角形,求点P坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com